Basic Paxos证明
Basic Paxos协议的证明过程
为什么Paxos三条约束下,就可以保证一致?The Part Time Parliament论文
约束
约束1:
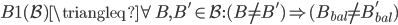
约束2:
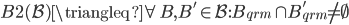
约束3:
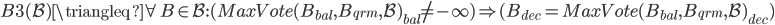
引理
如果 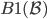 ,
, 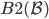 ,
,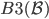 三个约束成立,那么
三个约束成立,那么
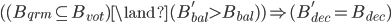
证明:
对于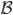 中的任何一个ballot B,定义
中的任何一个ballot B,定义 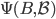 为
为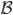 中比B的bal大且dec不等于B的ballot:
中比B的bal大且dec不等于B的ballot:
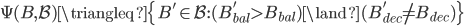
引理的条件表示B是一个成功的ballot。假设后续有ballot的bal更大,但是dec不等于这个成功的ballot的dec,即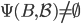 。下面我们用反证法。
。下面我们用反证法。
取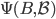 中bal最小的元素,设为C。
中bal最小的元素,设为C。
因为 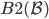 ,所以有
,所以有 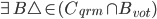 。
。
记vote 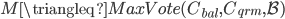 。由于
。由于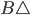 这个vote存在,所以
这个vote存在,所以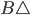 是M在取max时的元素之一。因为
是M在取max时的元素之一。因为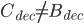 ,所以vote M与vote
,所以vote M与vote 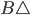 不是同一个vote。因此,
不是同一个vote。因此,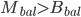 并且
并且 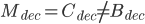 。那么,就一定存在另一个vote
。那么,就一定存在另一个vote 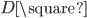 ,使得M=
,使得M= 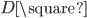 。
。
考察M(即 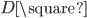 ):
):
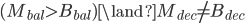
所以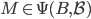
又,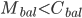 ,所以M是
,所以M是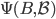 中比C还要小的元素,这跟C的定义矛盾。因此不存在这样的C。
中比C还要小的元素,这跟C的定义矛盾。因此不存在这样的C。
THEOREM 1
如果 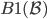 ,
, 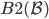 ,
,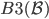 三个约束成立,那么,
三个约束成立,那么,
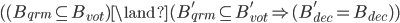
证明:
如果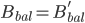 ,那么根据
,那么根据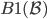 ,结论是平凡的。
,结论是平凡的。
如果 ,则根据引理显然成立。
,则根据引理显然成立。
THEOREM 2
设b是一个ballot number,Q是priest集合,满足条件: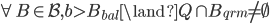 。
。
如果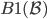 ,
, 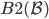 ,
,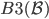 成立,那么,存在一个新的ballot
成立,那么,存在一个新的ballot 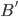 ,
,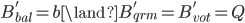 ,使得加上这个
,使得加上这个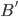 之后的
之后的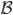 ,仍然保持三个约束
,仍然保持三个约束 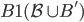 ,
,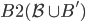 ,
,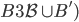 成立。
成立。
证明:
要证明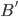 存在性,构造一个
存在性,构造一个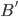 即可:
即可:
如果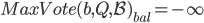 ,
,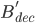 取任意值,否则取
取任意值,否则取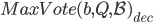
这个证明过程也表明了为什么Paxos需要prepare和accept两个阶段,因为要保持一致性,proposer就必须先得到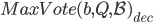 ,然后拿这个值来发起accept请求。同时,也指明了acceptor收到prepare请求时要做哪些承诺来保持一致性。
,然后拿这个值来发起accept请求。同时,也指明了acceptor收到prepare请求时要做哪些承诺来保持一致性。
acceptor q要持久化如下两项内容:
1. 有proposer要获得 ,
, 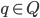 ,acceptor q在回应了该proposer response="
,acceptor q在回应了该proposer response="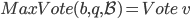 "之后,需要确保q对于
"之后,需要确保q对于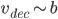 之间的accept request不能再vote了,所以要持久化
之间的accept request不能再vote了,所以要持久化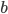 。
。
2. 持久化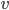 ,包括
,包括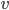 的decree和user value。
的decree和user value。
1 条留言 访客:0 条 博主:0 条 引用: 1 条
来自外部的引用: 1 条