《Distributed consensus revised》 Heidi Howard
整篇论文151页,粗略通读了一遍,主要是了解各个变体的基本思路和正确性直觉的理解,更形式化的证明基本上都跳过了。
这里假设读者对Basic Paxos有了一定了解,看过Lamport的那篇原始论文。另外我这里行文术语基本沿用原始论文的说法,跟这篇论文稍有差异,不过如果熟悉Basic Paxos的话,应该很容易对应起来。
导读
FLP定理已经证明了在异步网络下,不存在一个完全正确的consensus算法(safety + termination)。
FLP定理证明过程表明,一个声称完全正确的算法在执行到马上就要达成consensus的时候,一个开启了上帝视角的敌手,只要将某一个进程失效,该算法就会失败(要么终止在不一致状态、要么终止不了一直在未决状态之间打转)。
所以我们看到的consensus算法都逃脱不了这样一个模式:先尝试执行一系列步骤,如果长时间没有结束,就怀疑被敌手阻塞了,然后再来一轮,只要敌手放松,总是有机会执行结束。
这个”轮”在Paxos里面就是ballot_number / proposal_id,在Raft里面叫term,在ZAB里面叫epoch,在PBFT里面叫view_number。本质上它们都是同一个东西。
在真实的场景下,进程失效虽然可能发生,但并不存在这样一个开了上帝视角的敌手主动去失效进程,所以实践上重试几次几乎总是可以执行结束。这也是为什么Paxos有活锁,但工程上仍然可以大规模应用。
FLP跟这篇论文是什么关系呢?
如上述,FLP导致算法需要一轮一轮地重试,但在重试的时候,首先要担心之前某一轮已经确认了一个值,所以本轮要先学习上一轮的状态,才能真正执行确认步骤。
这篇论文说的就是从上一轮学习过程(或者叫上一轮到下一轮的信息传递过程)中,quorum的约束可以如何放松?
Classis Paxos算法下的”all quorums will intersect”是能够完成信息传递的充分条件,但不是必要条件,这也是这篇revised文章可以放松的直接原因。
论文Chapter1,2都是背景知识,Chapter8总结过于笼统,所以主体内容还是Chapter 3~7。这里大致罗列一下内容。
主旨内容一句话总结:因为要解决上一轮到下一轮的信息传递,所以要求是上一轮的accept phase和下一轮的prepare phase要有交集。这也是为什么${\scr{Q}}_{phase}^{epoch}$有上下标两个维度。4.2节的约束 $$\forall Q \in {\scr{Q}}_1^e, \forall f \in E: f < e \Longrightarrow \forall Q’\in {\scr{Q}}_2^f: Q \cap Q’ \ne \emptyset$$ 说的也还是这句话。根据这一主旨,可以有各种各样的放松方式。
Chapter 3 Known revisions
这一节主要是讲的一些小的、比较直观的改进。
3.1 Negative response:Basic Paxos中,acceptor只会返回正面的prepare response和accept response,不满足条件的proposer会等超时换epoch重试。这里可以改进成如果acceptor发现条件不满足,可以返回一个negative response,告知proposer。一个proposer如果收到多数派的negative response,那就确定本epoch下,自己以后也不会成功,所以可以立即发起换epoch重试,不用再漫长的等待。
3.2 Bypassing phase two:如果proposer在prepare phase收到了多数派的prepare response是相同的,那么accept phase是可以省略的。也就是说,在Basic Paxos算法下,从上帝视角看,在某个时刻,如果存在一个系统快照下,多数派的acceptor的accept proposal相同,该proposal的值就已经被确定是会被chosen的(只是可能还未被任何进程知晓)。
3.3 Termination:接上个improvement,如果某个值已经被chosen,那么,可以让acceptor知晓这一事实,然后新epoch的proposer在prepare phase就可以提前知晓这一事实,不必执行accept phase。
3.4 Distinguished proposer:如果两个proposer互刷freshness,可能导致Basic Paxos活锁,以致no progress。所以可以改进成先用其他选举办法挑一个proposer作为leader,只有他能提议。
3.5 Phase ordering:这里说了一个observation,要确认的value是在prepare phase结束后才确定的。
3.6 Multi-Paxos:Multi-Paxos是Basic Paxos在decree id维度的扩展,可以这样做的根本原因是proposer执行prepare phase的时候,不需要知道自己将来在accept phase想要确认的值,所以Multi-Paxos执行成功完一轮prepare phase,对于足够大的decree id,是能够自己决定要确认的decree的。
3.7 Role:工程应用中,很多情况下一个进程既是proposer,也是acceptor,这样可以减少不必要的一个proposer-acceptor间网络通信信道。
3.8 Epochs:一个proposer的epoch工程实现上一般要求单调递增,即使crash-recovery之后,也要保持,所以每次epoch都要持久化到本地防回退,但这里可以优化为持久化一个比较大的epoch,不必每次持久化。本质上epoch只要求unique、comparable就是充分的了,没有要求连续。
3.9 Phase one voting for epochs:接上,这个改进是为了允许不同的proposer使用相同的epoch(于是任何一个proposer可以使用任何epoch,放松这个要求可以提供一些改善的想象空间)。这个改进要求在accept phase要对epoch关联一个属主proposer(注意每个acceptor对同一个epoch可能关联不同的proposer)。
3.10 Proposal copying:如果一个人acceptor收到accept request(e, v),那么(e,v)这个对应关系实际上跟谁提出来的也没多大关联,所以可以被其他proposer接力使用。
3.11 Generalisation to quorums:quorum的泛化,见4.1节。
3.12 Miscellaneous:
Learning:学习chosen value。
Messaging:消息传递策略等misc。
Stricter epoch conditions:原文给了两个例子,我没继续看为啥要搞得太严格,感觉没大必要。
Fail-stop model:如果节点fail后无法恢复,acceptor可以不用持久化自己的承诺,因为持久化的目的主要是要防止acceptor说错话(非拜占庭错误下只有fail一种情况可能搞错,进程的执行逻辑是诚实的)。
Virtual sequences:如果是在确认一组值,可以做batch,比如index 10~15当成一个virtual index。
Fast Paxos:Proposer->Leader->Acceptor->Learner 中省略Leader的网络一跳,但要处理多个Proposer冲突情况,这个还比较复杂,不展开了。
Chapter 4 Quorum intersection revised
4.1 Quorum intersection across phases
基本的思路是prepare phase的quorum Q1要和accept phase的quorum Q2有交集就行,两个phase的quorum之间可以不相交。
以前写过一篇关于flexible paxos的博客,更详细一些,感兴趣的读者可以跳过去看看。
4.2 Quorum intersection across epochs
将$$\forall Q\in {\scr{Q}}_1^e, \forall f \in E, \forall Q’ \in {\scr{Q}}_2^f: Q\cap Q’ \ne \emptyset$$
放松成$$\forall Q \in {\scr{Q}}_1^e, \forall f \in E: f < e \Longrightarrow \forall Q’\in {\scr{Q}}_2^f: Q \cap Q’ \ne \emptyset$$
也就是说,之前条件里面quorum是跟epoch无关的,现在关联上之后,条件可以放松:如果有人执行过accept phase,后面其他人可能成功的prepare phase (e > f) 必须获知这一事实,也就是必须要跟前面这个accept phase的acceptor集合有交集。这里正是整篇文章的主旨所在。
4.3 Implications
4.3.1 Bypassing phase two
同3.2节类似,可以理解为3.2节基础上又增加”quorum引入epoch”。
4.3.2 Co-location of proposers and acceptors
Co-location of proposers and acceptors是指假设每个进程都既是proposer也是acceptor。在这个场景下,有些quorum变体。
All aboard Paxos:假设所有进程都正常,那么可以一轮就达成consensus。因为我们如下构造:Q2是全部进程的集合,prepare phase可以仅通过访问本进程的状态来完成。
Singleton Paxos:跟All aboard Paxos对称地,可以让Q1是全部进程的集合,而且结合3.3节提前结束的改进。
Majority quorums for co-location:大致思路是epoch按照round robin方式分配,并且是所有包含对应的副本在内的简单多数派集合,然后可以根据4.2节定义的条件推算。
4.3.3 Multi-Paxos
略,这个讨论的也比较多了,实践方面可以参考白哥写过的一些介绍。
这里又额外说了下4.2节所描述的quorum size的调增。简单地说,Q1小则可容忍faulty的acceptor数量越大,但一次accept就要更多acceptor参与,延迟因木桶效应就可能越大,反之同理可推。
4.3.4 Voting for epochs
略。3.9节演化过来的。
Chapter 5 Promises revised
如果在某时刻,某个proposer得知了prepare response(e,f,v),那么对于该proposer的这一轮e来讲,f之前的所有轮的Q2都已经不重要了,因为这个v已经确认是小于等于f的所有轮中的最新的结果了。
所以,e轮在prepare phase能获得最新结果的充分条件是:
$$\forall Q \in {\scr{Q}}_1^e, \forall g\in E: f<g<e \Longrightarrow \forall Q’\in {\scr{Q}}_2^g: Q\cap Q’ \ne \emptyset$$
Chapter 6 Value selection revised
6.1 Epoch agnostic algorithm
这个变体方案是修改了value selection的方法,在Classic Paxos中,value selection就是原始论文里面提到的MaxVote:即收到的prepare response集合中epoch最大的那个proposal的值,这个计算过程也很简单,就是遍历这个prepare response集合。
Epoch agnostic algorithm的修改是什么呢?它不再是像MaxVote一样按proposer粒度计算,而是按照Q2集合中元素Q的粒度计算。本质上是尝试逐个否定Q2的每个元素Q的方式,来排除一些val候选值。这个方法正确性的直觉是:真正被chosen的val是不会被否定掉的。
举个例子:5个acceptor,简单多数派的quorum system,如果某时刻系统状态为:**a1{p1v1}, a2{p2v2}, a3{p3v3}, a4{nil}, a5{nil}**。如果按照Classic Paxos的MaxVote,则一定得到v1/v2/v3中的某个值,但我们实际上可以确定v1/v2/v3都没有被chosen,按照epoch agnostic algorithm的Value selection算法,得到的就是nil。
6.2 Epoch dependent algorithm
前面Epoch agnostic algorithm方案只能针对quorum跟epoch无关的情况,例如4.2 Quorum intersection across epochs这个算法下就不能用了。这一节就是介绍了带epoch的改进版本。
Chapter 7 Epoch Revised
7.1 Epochs from an allocator
这个思路很简单,epoch分配交给特定的节点来做,epoch定义成(vid, sid),其中vid每次重启都要+1(因此要持久化),sid可以是个简单计数器,不需要持久化。
7.2 Epochs by value mapping
这个思路是说,反正是只想保证同一个epoch下不会有多个proposer提议不同的value,那么可以直接用value来定义epoch。概念上等价于有一个预先定义好的映射关系value -> epoch。文中举了一个非常tricky的例子,略。
但这样一来,像multi-paxos这种一次给无穷多个value进行prepare的思路就不好走了。
7.3 Epochs by recovery
考虑去掉一个epoch下只能提议一个value的限制。那么在4.2节的算法下,可能出现两个value被Q2中两个不相交的的quorum确认。这个问题可以通过限制Q2中的各个quorum都要相交避免。
不过还有问题:相同epoch不同value,可能导致value被覆盖写。这个问题可以通过限制accept,如果本地accept过epoch下的value,只有epoch和value都相同才accept,否则拒绝。
不过这又带来一个问题,在value selection时,proposer收到一个epoch下的两个不同值,它要选哪个来提议呢?因为其中一个可能已经chosen,所以自己根据本地信息来决策选一个是不靠谱的。
这个问题通过再加强quorum交集来解决:
$$\forall Q \in {\scr{Q}}_1^e, \forall f \in E: f < e \Longrightarrow \forall Q’, Q’’\in {\scr{Q}}_2^f: Q \cap Q’ \cap Q’’ \ne \emptyset$$
事实上这个相交要求已经太强了(如果是简单多数派的话,Q+Q-N+Q>N,可知Q>2N/3)。
7.4 Hybrid epoch allocation
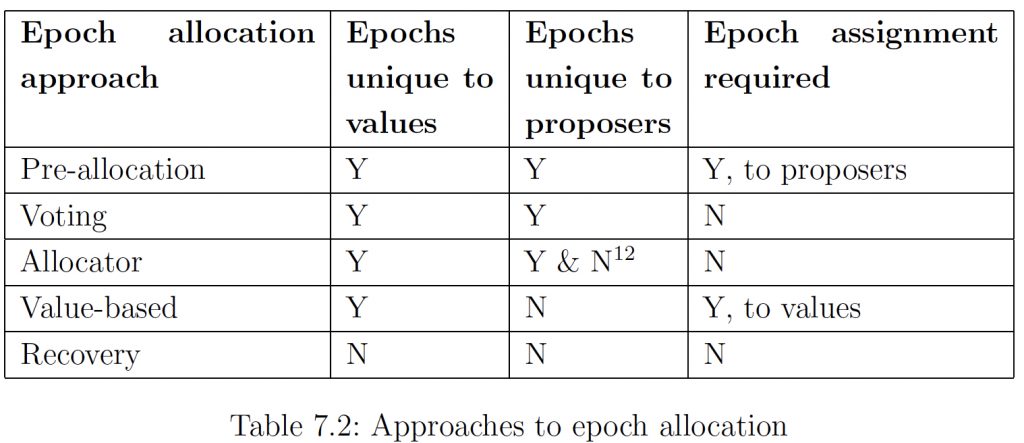
这节介绍混合的方案,略。
不过话又说回来,这篇论文整体上还是偏理论分析,除了multi-paxos等之前就有的变体算法,这篇论文提到的新的变体算法似乎没有什么实用价值,至今还没见过什么生产场景需要搞这么复杂的quorum system。
扫描二维码,分享此文章
