VLDB 18’  Content-Aware Lock Scheduling for Transactional Database

相关的证明在 Contention-aware lock scheduling for transactionaldatabases.Technical Report,

锁是TP系统中的核心组件之一，但对事务在锁方面的调度研究却比较少。

比如事务t1已经持有了某个lock，另外有t2, t3 … 因为申请同一把锁而阻塞，当t1提交释放锁（2PL）时，应该将锁给哪个事务呢？大部分系统用的都是FIFO，这意味着申请锁的一批事务的优先级都是一样的。

论文提出了新的锁调度算法LDSF，并证明了其最优性。

问题描述

$T$ : 事务对象集合

$O$ ：锁对象集合

图 $G=(V,E,L)$，其中 $V=T \cup O, E\subseteq T\times O \cup O \times T$

对于 $t\in T, o \in O$：

• $(t,o)\in E$ ： if $t$ is waiting a lock on $o$
• $(o,t)\in E$ ： if $t$ already holds a lock on $o$

$L:E\to {S, X}$ 用来表示锁类型：

• $L(t,o)=X$ ：$t$ is waiting a X lock on $o$
• $L(t,o)=S$ ：$t$ is waiting a S lock on $o$
• $L(o,t)=X$ ：$t$already holds a X lock on $o$
• $L(o,t)=S$ ：$t$ is waiting a S lock on $o$

假设无死锁（或死锁被单独的死锁检测模块发现并解决）。

调度算法：$A=(A_{req}, A_{rel}): G\times O\times T\times {S, T} \to 2^T$

设事务未来的执行时间是随机变量，期望是$R$。

设 $l_A(t)$ 是事务t在调度算法A下的总延迟，包括自己的执行时间和等待锁时间，它也是随机变量，其期望记为$\bar l_A(t)$

设 $\bar l(A)$是算法A下的所有事务平均延迟，即 $\bar l(A)=\frac{1}{|T|}\sum_{t\in T} \bar l_A(t)$

那么，优化目标是找到一个算法A，使得$\bar l(A)$最低。

注意到$A_{req}$是平凡的，我们只关注$A_{rel}$。

调度问题是NP-Hard

Thereom 1 ：给定G，当对象o上的锁释放时，选择哪个事务获取这把锁来使得目标最优，该问题是NP-Hard问题。即使所有事务的执行时间相同且不再申请新的锁，问题仍是NP-Hard。

几种简单的调度算法

文章描述了几种简单的冲突感知的调度算法。

Most Locks First

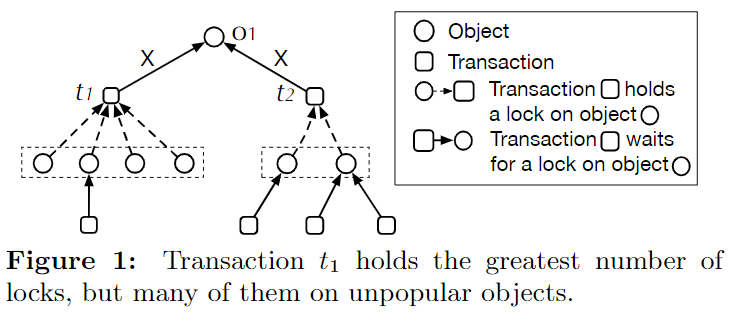
想法：持锁最多的事务优先。

问题：这种思路蕴含着将所有锁都视为相同优先级，但实际情况不是这样，比如热点行的锁影响更大。

Most Blocking Locks First

想法：只计数那些阻塞其他事务的锁，哪个事务持有这种锁越多，它就优先。

问题：直接被依赖的事务可能持有的锁不多，但是深度可能更深，进而影响的事务其实更多。

Deepest Dependency First

想法：被依赖子图越深，事务优先级越高。

问题：同样深度高不代表会block更多事务。

到这里，最优方案呼之欲出了。

论文给出了更优方法：Largest-Dependency-Set-First（LDSF）

Largest-Dependency-Set-First

定义$g(t)$是依赖事务t的所有事务的集合。

LDSF算法过程：

Theorem 2：只有X锁时，LDSF是最优的。

因为当一把锁给t1而不是给t2时，t2依赖集合中的事务全部都要等t1，反之亦然。

这就和 “*你一个人耽误一分钟,全班五十个人,你就耽误五十分钟!*”一样的道理。LDSF的意思就是既然要耽误了，就耽误一个人数少的班级。

Theorem 3：有S锁时，LDSF的跟最优结果最多相差常量系数

Splitting Shared Locks

在有S锁的情况下，LDSF算法是将所有申请S的事务当做一个事务来跟申请申请X锁的一个事务进行比较优先级。

这个思路的合理性在于申请S锁的若干事务确实是允许同时申请到该S锁并继续执行，但不合理性在于S的释放取决于这些事务中最后一个释放S的事务，如果申请S的集合比较大，实际上时间可能会比较长。

设$R_{i}^{rem}$是事务$t_i$剩余执行时间的随机变量，那么释放S锁的时间是其中最慢的事务的对应的时间，也就是 $R_{max,m}^{rem} = max { R_{1}^{rem}, R_{2}^{rem}, … , R_{m}^{rem}}$。这个值自然也是随机变量，并且它还有如下性质。

Lemma 4. if $\sigma_{k+1}^2 >0$，则 $ \bar R_{max,k}^{rem} <\bar R_{max,k+1}^{rem}, for 1 \le k \lt m$

很自然，新加一个随机变量（所有随机变量值域相同）再算最大值，肯定严格更大，除非值域取值为单个值。

定义delay factor $f(m)=\frac{\bar R_{max,m}^{rem}}{\bar R^{rem}}$，则有

C1. $f(1)=1$

C2. $f(m) < f(m+1)$

C3. $f(m) \le m$

C3是指上限等价于所有S锁事务串行执行的情况。

Theorem 5:  不使用 f(m)的调度算法一定弱于或者等于某个使用 f(m)的调度算法。

假如有一个使用f(m)知识的调度算法$A_{-f}$，则存在一个使用f(m)知识的算法$A$，且 $\frac{A_{-f}}{A}=\omega(1)$

基于此，论文提出了 bLDSF。

bLDSF算法

从衡量 speed of progress 的角度出发，当某个对象的X锁释放了，如果 $t^x$ 获得了X锁，则speed of progress是 $\frac{|g(t_x)|}{\bar R}$，如果一批申请S锁的事务申请到了，则speed of progress为 $\frac{|\bigcup_{i=1}^{k}|}{f(k) \bar R}$。

bLDSF算法如下：

Implementation0

近似计算

实现上需要实时遍历依赖图或者每次事务被阻塞或释放锁时维护依赖集合。这个成本就比较高了。

实现上采用如下的方式计算：当事务t未持有锁时，$|g(t)|=1$；否则 $|g(t)|\approx \sum_{t’\in T_t}|g(t)|+1$。

考虑到事务集合之间可能有交集，所以上述计算结果并不完全准确。

另一个问题是 bLDSF中如何计算$k$。

近似计算方法：先将事务按照依赖集合大小降序排序，然后计算找到使q最大的k。

避免饥饿

如何避免X锁一直加不上而饿死？

解决方法：调度中加一个单向barrier，只允许X向前调度，不允许S跨到X前调度。

其他

MySQL 8.0.3已经基于该算法做了实现，效果不错。

总结

锁调度被研究的比较少，这篇论文做了比较细致和理论化的分析，MySQL官方在8.0.3版本上做了实现且默认开启，并且效果不错。