分布式系统一致性协议里面有一个FLP impossibility的结论,这个结论是说,在分布式系统中,异步网络(消息延迟可能任意大或丢失,消息可能乱序),只要有一个进程失效(进程死亡或者足够长时间不响应),就不可能设计出一个确定性的一致性协议。
该结论由Fisher、Lynch、Paterson三位分布式系统领域的科学家在1985年在论文Impossibility of Distributed Consensus with One Faulty Process证明。
本文记录一下学习笔记。
模型概述
分布式系统异步网络
异步网络:消息延迟可能任意大或者丢失,消息可能乱序,无同步时钟可用。
进程失效:进程死亡或者足够长时间不响应。
一致性问题简化模型
每个进程初始时记着一个值0或1,根据特定的一致性协议,接收消息、改动该值、并发送消息,当进程进入decide state时,其值就不再变化。所有nonfaulty的进程都进入decided state时,协议成功结束。这里放宽到有一部分进程进入decided state就算协议成功。
一致性协议P的模型描述
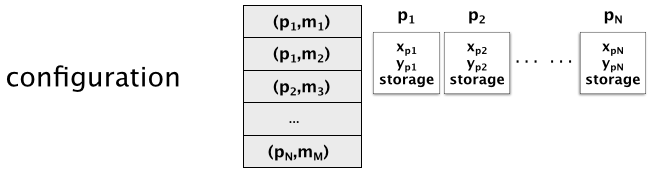
进程状态:异步分布式系统中N(N>=2)个进程,每个进程p有三个状态部件:1bit的输入寄存器xp、1bit输出寄存器yp(取值0/1/b,初始为b表示未设置过)、足够大的内部存储。进程可以从一个状态转换到另一状态。输出寄存器一旦从b设置成了0或者1就不能再更改。
消息:进程之间通过消息通信,消息记作(p,m),意为发送给进程p的内容为m的消息。系统有一个message buffer,存放了所有已经发送的消息。消息的发送定义为向message buffer中放置一个消息,接收定义为从message buffer取出发送给本进程的任意一个消息(没有消息就返回空标记)。如果某个进程p执行足够多次的接收消息操作,则最终message buffer里面发送给p的所有消息最终会被取出。异步网络下,即使message buffer里面有p的消息,也允许p执行接收消息操作时返回有限次的空标记,协议遇到空标记不做任何处理。
configuration:一个configuration包括N个进程的状态,以及message buffer。
initial configuration:N个进程的状态都是初始状态,message buffer为空。
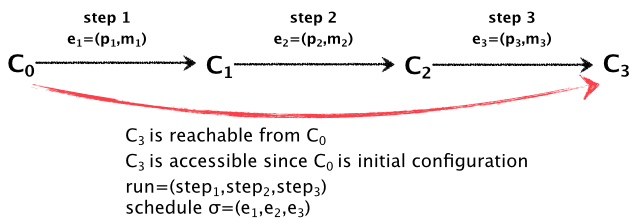
step:某个进程做一个基本操作(接收一次消息,并根据协议处理该消息,即改动本进程内部状态,发送消息给其他进程),将系统确定性地从configuration C转换到另一个configuration e(C)。一系列的step称之为一个run。
event:e=(p,m) 某个进程接收到某个消息并处理。
schedule:从C开始的schedule定义为从C开始的一个有限或者无限的事件序σ,如果σ是有限的,定义σ(C)为C应用了这一系列事件的结果,称σ(C)是可以从C可达(reachable from C)。这一个时间序列称之为run。如果一个C是可以从initial configuration可达的,就称C是accessible的。
如果configuration C中存在某个进程p处于decision state,且vp=v,则称C有decided value v。如果一个一致性协议P满足如下两点,则称之为P是partial correct的:
条件1:所有accessible的configuration都有相同的decision value。
条件2:对于v∈{0,1},至少有一些accessible configuration有v的值。
条件2是说,协议P不能是平凡的,凡是被提出来的值,都有可能成为decision value。例如,我们设计一个协议,这个协议要从{0,1}中选出一个一致的值,协议设计为,什么都不管,所有进程都只选择0,那这样的协议是不满足条件2的。
当然协议还要是可终止的。
admissible run:一个run中,如果最多只有一个进程是faulty,发送给其他nonfaulty的进程的消息都被处理了,那么这个run是admissible的。
totally correct:即使有一个faulty的进程,协议P仍是partial correct的话,那么P就是totally correct。
证明过程
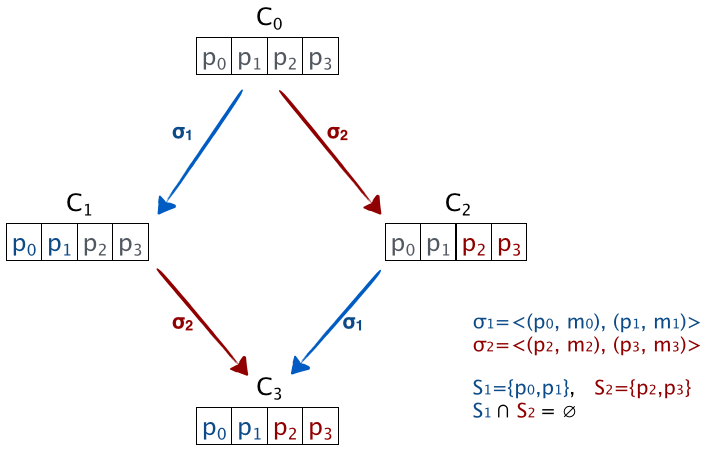
Lemma 1: suppose that from some configuration C, the schedules σ1、σ2 lead to configuration C1, C2, respectively. If the sets of processes taking steps in σ1 and σ2 , respectively, are disjoint, then σ2 can be applied to C1 and σ1 can be applied to C2, and both lead to the same configuration C3.
引理1:从C开始,分别经过σ1到达C1,经过σ2到达C2。如果σ1和σ2中各自的进程集合没有交集,那么,从C1上应用σ2和从C2上应用σ1会到达相同的configuration。
这个引理说的是,如果两个操作序列操作的是不同的进程集合,那先执行哪个序列结果都一样。这个是显然的,当然,这里要注意到C经过某个e,结果是确定的。
univalent/bivalent:从C开始,达到的所有decided configuration的decision value的集合定义为V,如果|V|=1,则称C是univalent(未来就确定了),|V|=2则称C是bivalent的(未来尚未确定)。也就是说,如果在C这里,往后看,如果将来只可能是0或者1中的一个成为decision value,那么C就是univalent的,否则,将来0和1都可能成为decision value,那么C就是bivalent的。
Lemma 2: P has a bivalent initial configuration.
引理2:P存在一个bivalent的初始configuration。
反证法,假设P的initial configuration都是univalent的(一些是0-valent,一些是1-valent)。
先描述一个记法:任意一个initial configuration的任意进程pi记为(xp=vi, yp=b, storage=∅),因为是initial configuration,所以yp和storage都是初始状态,将C=< p1p2..pN>简记为xp1 xp2…xpN。
定义两个initial configuration C1, C2是adjacent:如果C1和C2只有一个进程的初始状态不同,那么C1,C2是adjacent的。
容易知道,所有的initial configuration都是直接或者间接adjacent的,形成一个图。
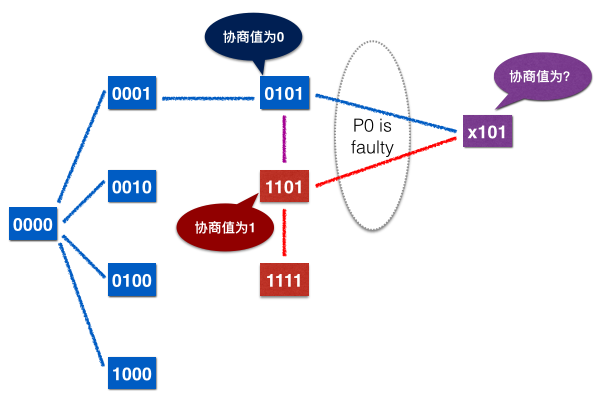
因为协议是非平凡的(条件2),一定存在两个configuration C0 C1,其中C0是0-valent,C1是1-valent的。这里假设C0=0000,C1=1111,那么在C0到C1的路径上,一定存在两个configuration Ca, Cb,其中Ca是0-valent,Cb是1-valent的,并且Ca和Cb是adjacent的(图中Ca=0101,Cb=1101),所以Ca和Cb只有一个进程是不同的(这里是p0)。现在假设p0是faulty的,那么Ca和Cb就是完全一样的状态,二者最终协商的decision value必然相等(二者都是univalent的),于是导出矛盾。
Lemma 3: let C be a bivalent configuration of P, and let e=(p,m) be an event that is applicable to C. let X be the set of configurations that reachable from C without applying e, and let Y = e(X) = {e(E) | E∈X and e is applicable to E}. Then, Y contain a bivalent configuration.
引理3:设C是一个bivalent的configuration,e=(p,m)是可以应用到C的事件。设X是从C可达并且未应用过e的configuration的集合,并构造Y = e(X) = {e(E) | E∈X and e is applicable to E}。那么,Y一定包含bivalent的configuration。
证明过程:
我们用反证法。假设Y中的configuration都是univalent的。
按照引理3中定义,我们有如下的示意图。
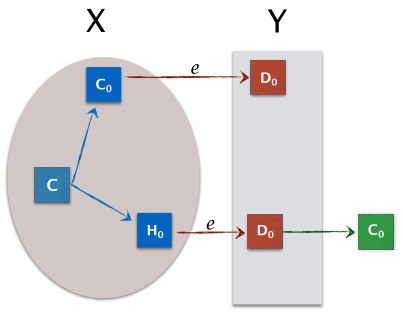
因为C是bivalent的,所以从C可以到达一个0-valent的decided configuration C0,也可以到达一个1-valent的decided configuration C1。C0和C1是对称的,我们只需要考察C0就行了。
如果C0∈X,则e(C0)=D0,D0是0-valent。
如果C0∉X,则取从C到C0中,接受e之前的configuration H0,那么,e(H0)=D0,D0是0-valent。
也就是说,Y中必有0-valent的configuration。同理可知,Y中也必有1-valent的configuration。
因为C属于X,且为bivalent,所以e(C)=D0是0-valent或者1-valent,假设是0-valent,那么一定存在一个从C可达的D1(C->Cs->Ct->D1),D1是1-valent的。
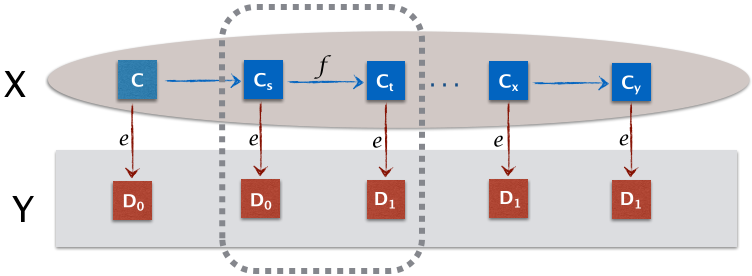
取图中虚线括起来的部分。我们得到下图。
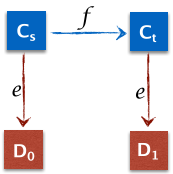
下面我们从该图推导出矛盾。
图中有两个消息e和f,他们操作的进程记为pe、pf。分为两种情况,pe=pf,pe!=pf,推出矛盾。
如果pe!=pf:
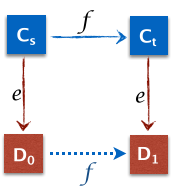
那么根据引理1,f(D0)=D1。D0是一个0-valent的configuration,而D1是一个1-valent的configuration。导出矛盾。
如果pe=pf(记为p):
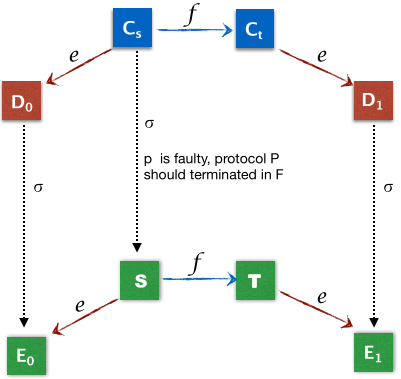
假设进程p faulty,协议容忍了p的faulty,仍然要保证能够从Cx出发经过某个schedule σ到达一个decided configuration,记为S。如图构造,σ(e(Cs))=E0,σ(e(f(Cs)))=E1,则按照引理1(σ与e/f操作的是不同的进程),e(f(S))=E1,e(S)=E0,说明S既可以成为0-valent,又可以成为1-valent,这与S是deciding configuration是矛盾的。
因此,集合Y中没有bivalent的假设是不成立的。
FLP Theory
根据引理3,我们发现从一个bivalent的configuration,总是能够变成另一个bivalent的configuration,而且这个过程可以无穷无尽下去。而引理2已经证明,initial configuration中bivalent的configuration是存在的。因此,算法总是有可能出现从一个初始的bivalent的configuration开始,从一个bivalent的configuration走到另一个bivalent的configuration(在马上要变成一个univalent的configuration时让某个进程crash),无穷无尽下去,无法停止。所以异步网络下,容忍一个进程faulty的一致性协议也做不到totally correct。(Any deciding run from a bivalent initial configuration goes to a univalent configuration, so there must be some single step that goes from a bivalent to a univalent configuration. Such a step determines the eventual decision value. We now show that it is always possible to run the system in a way that avoids such steps, leading to an admissible nondeciding run)。
上面的证明方法是用反证法,假设存在一个进程的faulty,证明算法可能一直处在bivalent configuration上。反证法有时候会不太容易建立直觉正确性。最近看了一本书,正面阐述了这个证明。
定义critical configuration :首先它是一个bivalent configuration,其次它的所有直接后继都是univalent的。
引理:一个consensus协议要想达成一致,必须走到一个critical configuration(注:这里假设转换图不存在环,如果有环,等价于协议本身的步骤有冗余)。这是因为如果不走到一个critical configuration,协议就一直在bivalent configurations之间转移。
假设某个critical configuration C的任意两个后继是C0(0-valent),C1(1-valent),即 e0(C)=C0, e1(C)=C1。那么e0和e1一定是作用于同一个进程p,否则e0(e1(C)) = e1(e0(C))矛盾。换句话说,所有从C转换到univalent configuration的转换,都是作用于p的。因此,让进程p faulty,协议就无法推进到一个univalent configuration了。
扫描二维码,分享此文章
