// 一篇闲扯的博文

Anna KVS官网对Anna的特性总结得非常到位：1. Crazy Fast, 2. Super-Scalable, 3. Flexibly Consistent。

这里只关注Flexibly Consistent这一项，讲讲Anna是实现灵活的consistency的背后的东西。

这篇博客算是论文导读，详细内容读者仍要仔细阅读论文原文 Anna: A KVS For Any Scale。

Lattice是什么

lattice是离散数学里面的概念，中文教科书上叫格。

格是一种有上下确界的偏序集（论文用的是只有上确界的半格，join semilattice），那偏序集是什么呢？

偏序集(partially ordered set, poset)：一个集合，以及该集合上一个偏序关系。

举个例子，集合$S={1,2,3,4,6,8,9,12,72}$，偏序定义成”可整除”，将偏序集用图来表示的话，就是这个样子。

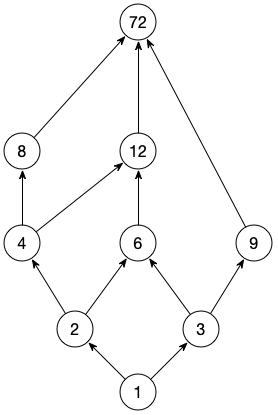
其中，1是下确界（所有元素都能整除1），72是上确界（72能整除所有元素），所以这个偏序集是一个格，自然也是个join semilattice。

非join semilattice例子：如果上图再加上一个元素64，集合中没有元素既能整除64，又能整除72，那么就不再满足上确界条件，因此也不再是一个join semilattice。

回顾Lamport讲的事件序（逻辑时钟），我们会发现，lattice来描述分布式系统里面事件的先后顺序是非常自然的，分布式系统中happen-before本身就是个偏序关系。

不过，论文中提到的lattice，用的是跟上述定义等价的代数系统里面的定义。

满足如下性质的代数结构叫格：

• 交换律 $a\sqcup b=b\sqcup a$
• 结合律 $(a\sqcup b)\sqcup c=a\sqcup(b\sqcup c)$
• 幂等律 $a\sqcup a=a$

论文使用这个定义，主要是为了贴切论文里面的说的merge动作。这里一个$\sqcup$运算(二元运算)就对应一个merge逻辑。再对应到前面一种定义方式的图示，可以理解成两个节点的最小的公共后缀节点（也就是最小公倍数，这也是两种定义方式等价的证明思路），比如$4\sqcup 6=12, 12\sqcup 6=12$。

注：关于merge动作（conflict resolution），可以先参考2007年Dynamo论文。

基于格怎么实现灵活的多种一致性

基本思路：系统中的不同组件上都可能存在若干个lattice用于描述偏序关系，灵活的一致性说白了，一是增加/减少lattice，二是增加/减少lattice的边（也就是增加/减少$\sqcup$运算，也就是增加/减少自定义解决冲突的逻辑）。

但要注意的是，只靠lattice这套框架是无法实现各种灵活的一致性的，因为尤其是在涉及到事务粒度的隔离级别/一致性的时候，lattice能做的只是些局部的逻辑（要注意到论文提到的coordinator-free）。lattice得是在系统为了实现特定功能而增加/减少/改造组件之后才能应用。例如，论文实现Read Committed的例子中有诸如要在事务提交前将数据buffer到client的临时缓冲区中操作。这也是我觉得这篇论文不干净的地方（否则那就厉害了，我们甚至可以基于lattice来一统consistency和isolation level的定义了）。

漫谈Consistency和Isolation Level

论文把Isolation Level和Consistency放在一块，统一到论文框架里面了（实际上，涉及到Isolation Level的时候，可能会把client buffer write这类非事件的逻辑也牵涉进来）。

那么，Isolation Level和Consistency有什么相似性？这是一个很zen-like的问题。我的看法是，二者其实都是用来衡量整个系统对客户端表现出来的异常程度的。从这个角度，也算给consistency和isolation level二者“混为一谈”找到了一个理由。

另外，希望业界大牛把这堆乱七八糟的东西理一下，该重新定义的重新定义，该抹掉的抹掉，省的以后讨论到这个话题，还得先对一下双方对consistency的理解是不是一样 :(