2.5节图
1. 图的搜索
图的搜索可以用BFS和DFS。
二分图问题描述如下:给定一个图,判定是否可以用两种颜色涂顶点,使得有边相邻的两个顶点不同色。
这个问题可以用DFS遍历求解。着色时,确定当前点的颜色后,当前点相邻的点的颜色也随之确定。在DFS遍历过程中,如果没有出现着色冲突,说明可以用两种颜色着色。
2. 最短路问题
最短路问题有多种算法,适用于不同的场景。
常用的Dijkstra算法用于求解没有负边的单源最短路的情况,其时间复杂度是O(|E|log|V|)。Bellman-Ford算法可以处理有负边的单源最短路问题 ,其时间复杂度是O(|V||E|)。Floyd-Warshall算法用于求解所有点对最短路问题(没有负权环),其时间复杂度是O(|V|3)。
Floy-Warshall算法的思路很有意思。
定义 dij(k) 为从i到j的,中间只经过{1,2…k}中的顶点的最短路径。
则:
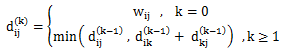
根据这个公式,可以写出非常简单的代码:
1 | D = W |
Roadblocks问题(P108):
求出图中指定的起点s和终点e之间次短路(第二短的路径)。
次短路问题和最短路问题类似。
假设s和e之间的次短路经过v,其中v到e有边。则,s到e的次短路只能是如下两种情况:
s到u的最短路加上边 v -> e
s到u的次短路加上边 v -> e
这样,我们要求出s到每个点的最短路和次短路。接下来,可以按照Dijkstra算法,在记录最短路的时候,同时记录次短路(多几次比较)就可以了。
3. 最小生成树
最小生成树常用的算法包括Prim算法和Kruskal算法。
Prim算法将顶点集合分为T和V-T,初始时T={v},v为任意顶点。每次都从跨T和V-T两个集的边中选出最短边的加入生成树中,直到T =V。时间复杂度是O(|E|*log|V|)。
Kruskal算法思想比较简单。为了取得最小生成树,每次都取剩余边中最小的边,如果这个边加入书中之后不会造成环,则加入,否则丢掉重新选择。时间复杂度是O(|E|*log|V|)。
Conscription招兵问题(P109)
问题描述:需征女兵N名,男兵M名,每征一人花费10000美元,但是如果已经征募的兵中有亲密的人,则花费会减少一定数值,该数值等于二人的亲密度。现给出若干个亲密度,求征兵最少花费。
把人当做顶点,亲密关系当做有权边,则问题变成了从图(可能不连通)中找一颗树(或者一个森林),使得该树(森林)的边权和最大。注意,因为招募过程中不会产生环路(环路中先招的那个人肯定得花10000美元,而不是10000减去某个亲密度)。
接下来,将边权值变为原来的相反数,用最小生成树算法求解。
扫描二维码,分享此文章
