Time, Clocks, and the Ordering of Events in a Distributed System
这篇论文Lamport发表于1978年,讨论的是分布式系统下的时钟和事件序问题。

图片来自《星际穿越》(计算机分布式系统环境与爱因斯坦相对论时空观具有本质相似性)
分布式系统的概念
分布式系统由不同的进程组成,不同进程可以经由消息通信。本文说的分布式系统是个广义的概念:一个互联的计算机网络是一个分布式系统;单台机器的CPU、IO部件、内存等也可被视为组成了一个分布式系统。事实上,如果相比组件内事件发生间隔而言,组件间的消息通信延迟不能忽略的话 ,这个系统就可以被视为分布式系统。
偏序关系
在分布式系统中,一个进程process内的多个事件,自然地具备事件的先后顺序,或者说一个process本身就是一个有先验顺序的全序的事件集合 a set of events with a priori total ordering。除了process内在的顺序,消息的发送和接收事件也是有因果序的。基于这两点,我们定义happen-before关系,写作$\to$。
Defination: happen-before关系$\to$,是一个分布式系统中事件集合上满足如下条件的最小关系:
(1) 如果$a$和$b$是同一个process内的事件,且$a$在$b$之前发生,那么 $a \to b$。
(2) 如果$a$是一个process发送消息事件,$b$是另一个进程接收该消息的事件,那么$a \to b$。
(3) 满足传递性,$a \to b \land b \to c \Rightarrow a \to c$。
如果 $a \nrightarrow b \land b \nrightarrow a$,那么,称$a$$b$是并发的。
根据定义,可以知道happen-before关系$\to$是一个系统所有事件集合之上的反自反偏序关系。
时空图space-time diagram可以直观地描述这个定义。
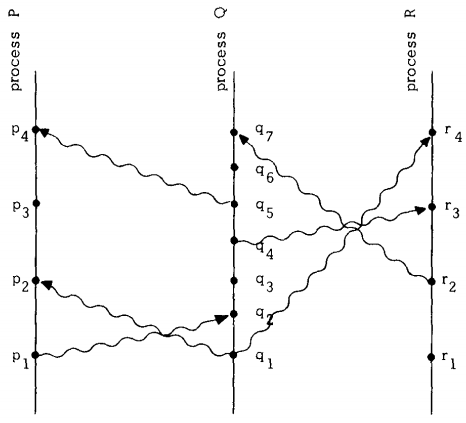
在图中,$a \to b$意味着从$a$可以沿着线到$b$,例如$p_1 \to r_4$。
这个定义的另外一种理解:$a \to b$意味着从$a$和$b$有因果序。例如$p_3$和$q_3$是并发的,意味着我们并不能推断两者的时序。
逻辑时钟Logical Clocks
概念上,时钟即给事件分配序号的方式。
定义$C_i$为进程$P_i$的时钟,$C_i\langle a \rangle$为进程$P_i$的事件$a$的序号。不关心哪个进程时,$C_i\langle a \rangle$记为$C\langle a \rangle$。该时钟与物理时钟physical time没有关系。
逻辑时钟怎么算是正确的呢?我们不能引入物理时钟来定义逻辑时钟的正确性,而应该是基于事件的顺序来定义正确性。如果两个事件有happen-before关系,时钟序号也应该与该关系一致,即Clock Condition。
Clock Condition: 任意事件$a$,$b$,如果$a\to b$,那么 $C\langle a \rangle \le C\langle b \rangle$。
该命题的逆命题不成立。
根据之前happen-before关系的定义,显然只要如下的两个条件C1、C2成立,Clock Condition就成立:
C1. 如果$a$,$b$是$P_i$的事件,且$a$在$b$之前发生,则定义$C_i\langle a \rangle \le C_i\langle b \rangle$。
C2. 如果$a$是$P_i$发送消息事件,$b$是$P_j$接收消息事件,定义$C_i\langle a \rangle \le C_j\langle b \rangle$。
那么,如何保证C1和C2这两个条件呢?只需要根据实现规则implementation rule IR1和IR2即可保证C1和C2。
IR1: $P_i$的两个连续事件之间要递增该process的$C_i$
IR2: $a$是$P_i$发送消息事件,那么消息$m$中携带一个时间戳$T_m=C_i\langle a \rangle$。$P_j$接收到该消息之后,将自己的逻辑时钟$C_j$推进到大于$T_m$的时刻。
我们在时空图上加上tick line虚线,就得到了下面的图。加虚线方式就按C1、C2来。同一process内连续的两个事件必须有一条虚线,消息传递的波浪线也需要交错一条虚线。
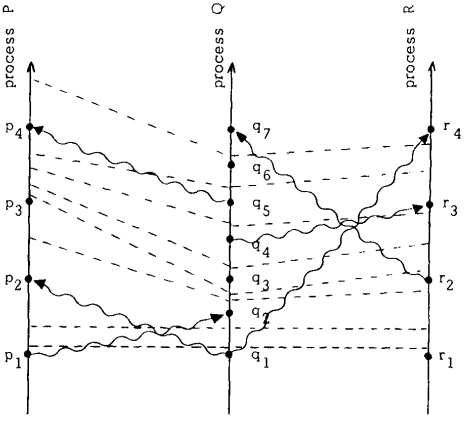
tick line实际上就是时空笛卡尔坐标系的时间轴,整理一下上图,即得下图。
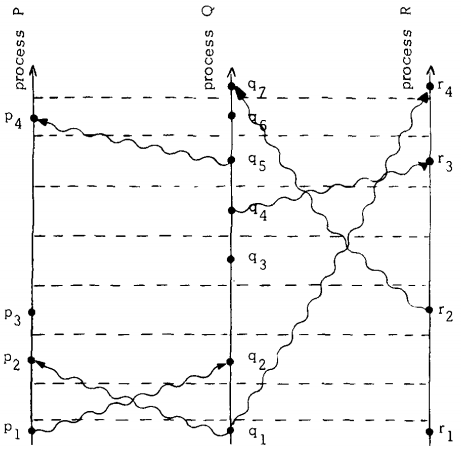
当然,也可以据此扩展画出3D时空图,tick line就变成tick surface了。
Ordering the Events Totally
我们将偏序关系扩展成一个全序关系。
我们构造一个关系$\Rightarrow$:
\begin{align} a \Rightarrow b \triangleq &(i) C_i \langle a \rangle \le C_j \langle b \rangle \&(ii) C_i \langle a \rangle =C_j \langle b \rangle \land P_i \prec P_j \end{align}
显然关系$\Rightarrow$是一个全序关系,且$\to \subseteq \Rightarrow$。
用全序关系解决分布式互斥问题
问题描述:一个分布式系统,多个进程共享一个资源。要求同一时间只有一个进程能够使用该资源。设计一个分布式算法,实现如下效果:
I. 已经获得资源的进程先释放,其他进程才能得到该资源。
II. 资源授予顺序需要按照申请的顺序。
III. 如果已经获得资源的进程释放了资源,其他想申请的进程最终能够获得该资源。
假设一开始资源已经授权给某个进程,假设消息通过ack和消息序号来保证消息不乱序、不丢失。
先考虑一个中心化的解决方案,用一个scheduler进程来协调,是不是能够完成任务?大难是在现有假设下无法做到。例如P0是scheduler进程,P1发了消息给P0申请资源,然后发消息给P2,P2收到消息后向P0发消息申请资源。显然,P1先于P2申请,但是P0可能先收到P2的申请。
那我们如何用全序来解决这个问题呢?
假设我们已经有了全序,那么剩下的问题就变成了让每个进程都知道其他进程的操作。
让每个进程维护一个请求队列,该队列只对本process可见。队列初始有一个元素 (T0:P0 request resource)。
算法按如下的5个规则运行,每个规则对应的操作都是一个事件。
- 如果Pi想申请资源,就要像所有其他进程发送消息 (Tm:Pi request resource),Tm是该消息的时间戳。Pi自己将该消息加到请求队列中。
- Pj收到(Tm:Pi request resource)之后,将消息放到队列中,并回给Pi一个ack消息,该ack消息也带有时间戳。
- Pi要释放资源时,将(Tm:Pi request resource)消息从它的队列中删除,并向其他进程发送消息(Tm:Pi release resource)。
- Pj收到消息后,从自己的队列删除(Tm:Pi request resource)。
- Pi如果发现队列中消息满足如下两个条件同时满足时,就认为自己获得了资源:
- (Tm:Pi request resource)在队列中,且在所有request resource消息中,全序中最小
- Pi收到过其他所有进程发过来的时间戳大于Tm的消息
值得注意的是,进程是否获得了资源的判定完全是个本地行为。
这五条规则是如何实现I,II,III的要求的呢?
因为任一进程都要把自己的请求,不管是申请资源还是释放资源,通知到其他所有进程。如果规则5(ii)成立,说明Pi已经得知了其他所有进程至少在Tm之前的所有请求状态。假设此时不应该是Pi获得资源而应该是Pj获得资源,则Pj申请资源的事件的逻辑时钟序应该小于Tm,因此在Pi本地队列中有这一个消息,而且该消息在全序关系中比(Tm:Pi request resource)小,这跟规则5(i)矛盾。所以Pi仅根据本地判定自己获得资源是符合要求的。所以要求I是满足的。
因为只有3和4会删除消息,所以除非Pi释放了资源,否则(Tm:Pi request resource)就会一直在消息队列中,且占据着全序最小的位置,其他进程是不会判定自己可以获得资源的。
因为我们是按照全序关系来判定的,而全序又是从偏序扩展来的,因此不会违背偏序定义的顺序。要求II因此满足。规则3、4在删除了(Tm:Pi request resource)之后,必定有另外一个进程Pj的申请消息会占据全序的最小值位置,而ack消息也能保证5(ii)成立。因此III成立。
这是一个分布式的算法:每个进程都遵守该规则,判定逻辑也只在本地执行,无需中心化的进程和中心化的存储。
该方案还可以从StateMachine的角度描述:
集合$S$代表所有可能的状态,集合$C$代表所有可能的命令,状态转移函数 $e: C \times S \to S$用于执行状态转移。每个进程都各自执行一系列的状态转移命令,而不同进程的命令序列由全序指明。
Anomalous Behaviour
考虑如下的场景:甲发了一个请求a给机器A,然后甲电话(电话而不是消息)通知乙,乙发送请求b给B。那么,虽然外部有a应该早于b,但是实际上在偏序关系中,a未必在b之前。
原因很显然,甲乙之间用电话联系起来的时序关系,并没有引入到我们之前讨论的偏序里面来,对于之前讨论的时序系统来说,这个关系是外部的关系。另外一个显然的事实是,仅根据原来偏序里面的信息,是无法解决这个外部问题的。
要解决这个问题,一种方式是将外部序引进来,将电话通知视为消息即可。另一种方式,称之为Strong Clock Condition。
Strong Clock Condition:
For any events $a, b$ in $\varphi$: if $a \boldsymbol{\to} b$, then $C\langle a \rangle < C\langle b \rangle$.
其中,$\boldsymbol{\to}$是在$\to$之外又引入了外部序的偏序关系。$\varphi$是系统内的事件集合。
论文提到$\boldsymbol{\to}$实际就是狭义相对论中的事件序。在狭义相对论中,不同的惯性参考系对一对无因果关系的事件的发生的先后顺序的观测结果可能是相反的,例如,飞船上看到事件1先于事件2发生,但在静止的地面观测到的可能是事件2先于事件1发生(这是宇宙中普遍存在的现象,由狭义相对论中时空本身属性决定的)。同样地,在分布式环境下,即使使用了物理时钟,我们也可以定义不同的事件序,也就是说,满足Strong Clock Condition的偏序关系不止一个。
物理时钟
我们现在引入物理时钟。
定义$C_i(t)$为在物理时间t时刻,$C_i$这个时钟设备的读数。为了方便讨论,除了时钟重设等时刻,$C_i(t)$都是连续可微的函数。
如果$C_i$这个时钟可以被当成真实物理时钟使用的话,那就要求两者的时间流逝速度差不多。即
PC1 Condition: 存在一个常量 $\kappa \ll 1$,满足:$\forall i: |\frac{dC_i(t)}{dt}-1| < \kappa$
通常石英钟的$\kappa \le 10^{-6}$。
除此之外,仅跟物理时钟比还不太够,各个时钟之间的差值也不能太大,即
PC2 Condition: $\forall i,j,t : |C_i(t)-C_j(t)| < \epsilon$
在PC1和PC2成立的条件下,里面的参数 $\kappa , \epsilon$ 满足 什么条件时,才不会出现前文所述的异常现象anomalous behaviour,也即才能保证Strong Clock Condition成立?
我们假设事件$a,b$满足$\boldsymbol{\to}$(粗体)关系,但是不满足逻辑时钟偏序关系,即Strong Clock Condition被违反。因为$\boldsymbol{\to}$(粗体)是逻辑时钟偏序关系的增强,显然只需要考察$a,b$是不同进程在相近的时间发生的事件这种情况。
设$a$发生在物理时钟$t$时刻,$b$发生在物理时钟$t+\mu$时刻。为了避免异常现象发生,需要保证 $\forall i.j: C_i(t+\mu) - C_j(t) > 0$,即真实的物理时间轴上后发生的事件,其逻辑时钟也靠后。由PC1、PC2、再加上这条可以推导出参数关系。
推导过程如下:
$|\frac{dC_i(t)}{dt}-1| < \kappa$
$1-\kappa < \frac{dC_i(t)}{dt} < 1+\kappa$
$ \int_t^{t+\mu}(1-\kappa)dt< \int_t^{t+\mu}\frac{dC_i(t)}{dt} dt < \int_t^{t+\mu}(1+\kappa)dt$
化简得 $C_i(t+\mu)-C_i(t) > (1-\kappa)\mu$
变形得 $(C_i(t+\mu)-C_j(t))+(C_j(t)-C_i(t)) > (1-\kappa)\mu$
$(C_i(t+\mu)-C_j(t)) > (1-\kappa)\mu - (C_j(t)-C_i(t))$
要保证$ C_i(t+\mu)-C_j(t) > 0$恒成立,即$(1-\kappa)\mu - (C_j(t)-C_i(t))$恒为正,
则要 $\epsilon \le (1-\kappa)\mu$ 要成立。
也就是说, PC1,PC2再加上 $\epsilon < (1-\kappa)\mu$ 条件,就可以保证,发生的物理时间点差值超过$\mu$的两个事件,Strong Clock Condition成立,异常现象不会出现。这个条件也是符合直观感觉的:两个机器上的本地时钟误差越大,Strong Clock Condition越不容易成立;两个机器本地时钟与绝对时钟推进速率偏差越大,Strong Clock Condition越不容易成立;外部事件间隔事件越长,Strong Clock Condition越容易成立。
那么下面问题就来了,如何设置本地的时钟,使得上面的PC1、PC2条件成立?
论文给出了两个实现规则IR1’和IR2’,并证明该实现规则下,PC1、PC2都成立。
假设消息发送到接收的延迟是$v_m$,并假设消息传递有个最小的延迟$\mu_m$,定义$\xi_m=v_m-\mu_m$为unpredictable delay。
IR1’:对于Pi,如果没有收到消息,那么要求$\frac{dC_i(t)}{dt}>0$。
IR2’:如果Pi在物理时间$t$时发消息给Pj,则消息携带的时间戳为$T_m=C_i(t)$,Pj在物理事件$t^{‘}$收到消息后,将本地时钟修改为$C_j(t^{‘})= max{C_j(t^{‘}-0), T_m+\mu_m}$
注意到,两条规则虽然用到了物理时间,但是我们并不需要真实得到这个值。IR1’和IR2’实际上是对IR1和IR2的一种特化。
论文最后给出了一个定理,该定理不仅确定了PC2可以满足,同时还给出了系统初始启动后多久才能同步的下限。
THEORY:将分布式系统视为有向图,节点为进程,有消息传递视为边,设该图的直径为d。假设所有消息$m$都满足$\mu_m<\mu$,其中$\mu$为常量。在IR1’、IR2’成立的条件下,PC1成立。
如果存在常量$\tau,\xi$,每$\tau$秒都有消息在unpredictable delay不超过$\xi$的情况下在有向边上传递,那么,PC2成立,且对于$t \le t_0+\tau d$ 都有 $\epsilon\approx d(2\kappa\tau+\xi)$,其中$\mu+\xi\ll\tau$。
证明比较繁琐,这里略掉。
结论
分布式系统的happen-before关系是个偏序关系,并且我们扩展为一个全序关系并用于分布式资源协调问题的求解。但是即使在全序关系下,会有异常情况发生,这里通过同步时钟来避免异常现象。
扫描二维码,分享此文章
