本文是 Why Functional Programming Matters的阅读笔记,用相对通俗的语言解读了这篇论文,并对我觉得重要的一些点做了一些解释,欢迎在读这篇论文的朋友留言交流。不得不说的是,这篇论文大量涉及到SICP这本书中的知识,所以如果能看过SICP再看这篇论文,相信应该会轻松很多。限于拙劣的智商,我只是囫囵读了一遍SICP,如果本文有错误,请各位读者留言指正。本文提到的SICP的参考章节页号是指对应于SICP中文版第二版这本书(应该是市面上最常见的那本)。
为什么函数式编程很重要
摘要:
随着软件变得越来越复杂,良好地组织软件也越来越重要。一个组织良好的软件更容易编写调试,这种软件提供了一组可以复用的模块(module),这也降低了未来编写代码的代价。本文将说明,函数式编程语言的特色,尤其是高阶函数和惰性求值(high-order function and lazy evaluation),将会对模块化非常有利。作为例子,本文还将操作list和tree,编写几个数值计算算法,实现一个alpha-beta启发算法(人工智能中关于博弈的一个算法)。因为模块化是软件开发成功的关键,所以函数式编程会在软件开发过程中具备很大的优势。
Introduction
函数式编程一个特点是不包含赋值语句,因此函数没有副作用,更类似于数学里面的函数。同样地,函数执行的时机也变得不重要了,毕竟函数执行没有副作用,一个函数必须在另一个函数之后执行这样的要求也没有意义了。论文中提到了引用透明(referential transparent),意思是说,变量和值可以随意代换,因为表达式在什么时候计算没有影响。
函数式程序设计人员声称函数式程序设计(为简化描述,后文用FP表示函数式编程)生产效率更高,因为FP程序更短。[看过Haskell写的qsort程序就知道这句话是对的]
与结构程序设计的对比
结构程序设计(例如C语言代码)一个重要的特征就是程序块(例如函数什么的),这种模块化提高了生产效率。
这篇文章还点明了一个重要的结论:模块化的过程是将问题分解成子问题,求解子问题,再将子问题的解结合(glue)起来的过程。怎么分解直接依赖于编程语言提供了怎样的结合方法。所以要增强模块化能力,需要提供新的结合方法。
后文所论述的高阶函数和惰性求值,正是FP提供的新结合方法,我们在读后文的时候,可以体会一下这两个特性带来的新的抽象和模块化。
将函数结合在一起
这一节首先介绍来了列表list,具体的内容参见论文原文,另外参考SICP第2章。
如果我想求出一个list中所有元素的和,可以这样写:
1 | sum Nil = 0 |
对上述两个式子,我们做进一步的抽象。注意到这两个式子表达的意思是,对于sum这样的一个操作,我们要提供一个空list对应的值,同时也要知道在将list拆成(n list’)时,我们应该如何处理这两部分。即: sum Nil = 0 sum ( Cons n list ) = n + sum list我们把这个过程抽象出来,记为foldr,foldr这个抽象需要额外的两个参数(这里是0和+),才能结合成一个新的对我们来说可以直接作用于list的操作(这里是sum)。
也就是说,
1 | sum = foldr (+) 0 |
而foldr所表示的抽象过程是:
1 | ( foldr f x ) Nil = x |
注:如果设定f为加操作,x为0,即刚才所说的sum。当然,这里加法写法跟通常不太一致,a + b在此处表达为 + a b这种操作符前置的形式。
我们将sum的过程抽象出来一个foldr,那这个foldr的威力何在?请看如下的几个例子:
1 | product = foldr * 1 |
当我们抽象出来一个foldr,就可以轻松地构造很多实用的代码!
再来一个:
1 | length = foldr count 0 |
这个 length跟上面的几个不太一样。差别在count函数。回顾刚才的foldr的定义,其中的f作用于两个参数上,一个是a,另一个是 ((foldr f x) l),所以两个参数类型可能是不同的,一个是列表元素类型,另一个参数与x是同一类型。例如,此处count作用于a n两个参数,其中a是列表元素,而n是整数(跟length定义中的0类型一致)。这和前面sum/product等稍有差异,可能会引起一点费解。
接下来是介绍map,map意思是对一个list的每一个元素,都执行一个操作,例如对每一个元素都加倍。因此map可以定义为:
1 | map f = foldr (Cons.f) Nil |
这里Cons.f是Cons和f复合(composition)的写法,其中(f.g) h = f(g h)。
所以,map f的意义为,将f作用于列表的第一个元素,并将结果与列表中除第一个之外的子列表的递归map f通过Cons组成结果列表。
从中可以看出,一个很小的模块化能力(foldr)能够实现各种实用的东西。
除了列表list之外,我们还可以定义树。
1 | treeof * ::= Node * ( listof (tree * ) ) |
简单解释一下这个定义式:*是类型;Node可以理解成针对树的关键字,它表达一个节点;listof是用Cons将若干子树串成list。
所以,形如图中的树
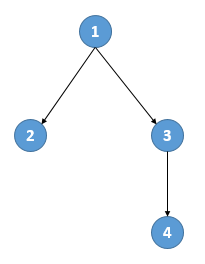
可以表示为:
1 | Node 1 |
这个表示是根据定义写出来的,其中Nil表示list结束。
如果理解有困难,可以参考“层次性结构”(SICP 2.2.2 P72)一节。
本文也解释一下这个表达式是怎么写出来的:
首先tree的定义是递归定义的,所以我们从叶节点开始写。
节点4是个叶子节点,没有子树,所以按照定义,这个tree的表达式是 (Node 4 Nil),同样,节点2表达式是(Node 2 Nil) ,记为subtree2。现在看节点3。节点3有一个子树,也就是说,它的子树列表有一个元素。这个列表的构建用到Cons,列表以Nil结尾,所以,节点3对应子树的表达式是(Node 3 ( Cons (Node 4 Nil) Nil )) 记为subtree3,同样的道理,整个树的根,也就是节点1,它的表达式是:Node 1 ( listof tree *) 即Node 1 ( Cons subtree2 subtree3 Nil)
即
1 | Node 1 ( Cons (Node 2 Nil) ( Cons (Node 3 ( Cons (Node4 Nil) Nil)) Nil)) |
写为多行:
1 | Node 1 |
读者或许对上面出现的Cons比较奇怪,这是因为通过Cons构造list的语法就是这么规定的(Nil也是这么来的),如果有list这样的关键字,可能tree写出来的表达式就会变得清晰很多。这个规定请参考“序列的表示”(SICP 2.2.1 P66),该章节开头就有张图和对应表达式,清晰易懂。
了解了tree的表达式,下面定义对树的操作的一个高阶函数 foldtree。
1 | foldtree f g a (Node label subtree) = f label (foldtree f g a subtree) |
按照tree的定义式,就可以理解这里定义的foldtree的意义了。
foldtree有四个参数,f g a和tree(还包括空树,没有root的子树列表)。其中
a表示对于空树的操作,应该返回的值(第三条);
g表示分别作用于子树之后返回的结果应该如何结合(第二条);
f表示作用于当前树的根节点和g的结果(第二条的结果)的操作(第一条)。
例如,sumtree = foldtree + + 0 ,意思是说,空树返回0,求和过程中,子树返回的结果也要求和,这个和还要和根节点相加。
1 | maptree f = foldtree (Node.f) Cons Nil |
将等号右侧表达式展开就可以知道,maptree实现的效果是对每一个Node用f处理,仍保持树原来的结构,这正是我们期望的maptree。
从上面这么多例子,我们看出,FP允许我们将函数表达为高阶函数和一些特化函数的组合(combination),而且这种方式具备很强大的能力。
将程序结合起来
FP提供的一个重要结合方法是可以将程序结合起来,f和g都是函数,g.f(复合)也是函数。g.f 等价于 g(f input)。这个表达式是说,f接受输入,计算出输出,并将该输出作为g的输入。在C/C++这类语言中,f需要先处理所有的input之后,才能开始g的执行,而在FP中,f和g是同步化进行的(run together in strict synchronization),只有当g需要一个新的输入的时候,f才处理一个输入并将输出交给g。因此f完全可以是一个不会终止的函数。这就是惰性求值(lazy-evaluation)。
值得注意的是,这里体现了一个很强大的模块化能力:将终止条件从循环体中分离出来。
有了惰性求值,我们可以将一些函数模块化为一个生成器(generator)和一个选择器(selector),生成器能够构建大量的解答,而选择器会选择其中一个。
当然,非FP语言增加惰性求值会不会使得这些程序更易用?答案是不是。惰性求值的威力依赖于程序员放弃了直接控制程序的各个执行部分的次序。
接下来是一些数值算法和AI中一个启发式算法。
Newton-Raphon平方根
Newton-Raphon算法计算n的平方根sqrt(n):
给定一个初始值a0,然后根据下式迭代计算一系列近似值。ai+1 = (ai+n/ai)/2
当ai+1和ai相差小于指定精度eps时,结束,ai作为sqrt(n)的近似值。
迭代抽象为:
1 | repeat f a = Cons a (repeat f (f a)) |
所以,Newton-Raphon算法产生的一系列近似值可以表达为:repeat (next n) a0
剩下的就是在这个一系列近似值上的选择,这里需要一个within函数。within定义如下:
1 | within eps (Cons a (Cons (b rest)) |
结合起来,就是sqrt a0 eps n = within eps (repeat (next n) a0)原文接下来是数值微分和数值积分的例子,道理是一样的,不再赘述。
AI中用到的一个alpha-beta启发算法
这个相比上面的数值计算算法要有趣一些。
Tic-tac-toe游戏规则:双方在3*3的方格中轮流画自己的符号,’O’或者’X’,先画出共线的三个符号者胜。
定义棋盘局面为position,每个position对应若干可以从当前position到达的新的position。所以,定义moves:
1 | moves :: position -> listof position |
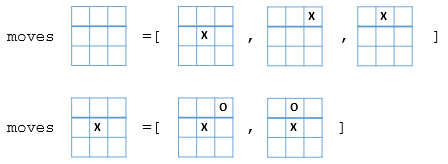
基于此,我们能够构造一个 gametree:
1 | reptree f a = Node a (map (reptree f) (f a)) |
多解释几句,reptree是构造树的递归结构,其中a为树根,f为从根能够通过f计算,能够达到的子树根。所以gametree p = reptree moves p。gametree产生的结果如图。
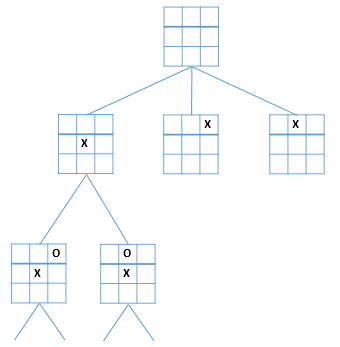
alpha-beta启发算法会向前多看几步,看看情况是有利还是不利。为此,我们需要给每一个position一个静态的对应的粗略估值,这个值反应position当前对哪一个玩家有利。举个例子,人机对战时(alpha-beta作为电脑一方),如果对电脑玩家有利,就记为1,如果对对手有利,就记为-1。
所以我们需要一个static函数:
1 | static :: position -> number |
因此,我们将一棵position树映射为一颗number树:
1 | (maptree static) gametree |
在思考如何下棋时,静态的值并不能反映当前棋盘position的真值(true value),因为这个静态值并没有反映出向前看的前瞻性。所以,一个position的真值应该由position的子树决定。所以对于电脑来说,算法会选择一个真值最大的子树,对于对手,会选择真值最小的子树。
最大和最小函数如下:
1 | maximize (Node n sub) = max (map minimize sub) |
当然还要加上空树的情况:
1 | maximize (Node n Nil) = n |
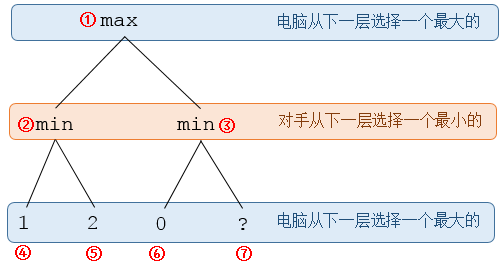
正如图中所表示的这样。因为电脑对手会在第二层中选择了最有利于它自己的策略,所以电脑算法计算最顶层的max的时候,依赖于第二层的min(对手的选择结果)。
现在我们可以尝试写出一个position对应的真值了:
1 | evaluate = maximize.maptree static.gametree |
这个式子反映了我们之前描述的那一堆东西,但是仍然存在一个问题。
如果树是无穷层的怎么办,或者,虽然是有限层数,但层数太多怎么办?
要把这些层都考虑进去是不现实的,所以我们将maximize执行的时候给它一个层数限制,向前看一定步数就可以了,一眼算到底是不现实的。
因此我们增加一个剪枝函数:
1 | prune 0 (Node a x) = Node a Nil |
这个定义就是刚才所描述的限制步数的过程,换言之,在尝试向前看一直看到最后的position不现实的情况下,我们做了些妥协,就向前看N步(例如5步)就不再往前看了。
所以,新的evaluate函数现在可以写为:
1 | evaluate = maximize.maptree static.prune 5.gametree |
evaluate函数是怎么计算的也是一个有趣的问题。我们当然不是先执行gametree构建整个树(即使树是有限大小的),而是在执行maximize的时候,按需构建这颗树中我们当前所关心的部分。这里就用到了惰性求值。如果没有惰性求值这种特性,我们是没法将这些函数通过这种方式折叠(fold,折叠成串)起来的。
alpha-beta算法还观察到了一个现象:在局面变为上图所示的情形时,显然,在这个图中,电脑应该选择②(也就是节点①真值为1,即节点④的1),而且这个选择完全不受节点⑦的真值**?**的影响。不受影响意味着可以剪枝,进而减少计算时间。
那么如何剪枝?在说明这个问题前,我们要先看为何现在的代码不能剪枝?琢磨一下,我们能够发现,问题出在maximize的定义上。maximize定义就是简单地max下一层的真值,而不能直接看到再下一层的数字。所以我们更改maximize(相应地,也改变minimize)的定义:
1 | maximize = max.maximize’ |
其中,maximize’定义如下:
1 | maximize’ (Node a Nil) = Cons n Nil |
在这个新改写的定义下,我们看到maximize能够看到minimize’。这意味着,maximize可以直接看到下下层的数字。
下面我们结合上图的例子看这个定义。
当我们maxmize Node 1的时候,上述定义中各个表达式的值分别是(此处假设?>0):
1 | n = 1 |
所以,
1 | maximize’ (Node 1 l) = mapmin [ [1,2], [0,?] ] = [ 1, 0 ] |
此时,需要重新定义mapmin来支持忽略不需要的子树(剪枝)。论文中给出的定义如下:
1 | mapmin (Cons nums rest) = Cons (min nums) (omit (min nums) rest) |
这个定义比较复杂,mapmin用到了omit,omit用到了minleq,我们仔细分析一下。
minleq定义告诉我们,minleq接受两个参数,一个是数字列表,另一个是数字pot,如果存在列表中某个数比pot小,就返回true,否则就返回false。
omit的定义告诉我们,omit接受一个数字pot和一个‘列表的列表’作为参数,omit会从前往后挨个看‘列表的列表’的每一个元素(列表),如果当前列表最小值比pot小,就直接忽略这个列表,否则就将这个最小值增添到结果列表中,并将pot改为这个最小值,用于后续的其他列表。
mapmin只是简单地调用了omit,给了pot一个初始值。
如果上面的解释看的比较晕,本文结合例子说明一下。还是上图的例子。
1 | mapmin [ [1,2], [0,?] ] |
omit 1 [[0,?]] 的计算有if分支,判断条件为minleq [0,?] 1,意思是说[0,?]的最小值比1小吗?此处返回true。所以omit 1 [0,?]走if分支,即
omit 1 [[0,?]] = omit 1 Nil = Nil
所以,mapmin [ [1,2], [0,?] ] = [1, Nil] = [1]
所以,这个过程更像是迭代,mapmin从前向后依次考察这个‘列表的列表’参数的每一个列表,若当前列表最小值大于pot,就用这个最小值更新pot,否则就忽略这个列表。
再举一个大一点的例子:mapmin [[1,2], [0,6], [3,5], [2,3]]= omit 1 [[0,6], [3,5], [2,3]]= omit 1 [[3,5], [2,3]]= [1, 3, omit 3 [[2,3]] ]= [1, 3]这里[0,6]和[2,3]被忽略了。
本文再结合游戏背景多解释一下这个例子。
当电脑在考虑如何选择下一步时(现在电脑能够看到下下层数字),电脑知道无论我选择哪一个,对手都会在此基础上选择最小的,所以,[[1,2], [0,6], [3,5], [2,3]]中只有各个子树中最小值(已标红)才需要考察,即[1,0,3,2],电脑当然希望选择这些最小值中最大那个,所以电脑从前向后看,第一个标红的是1,所以电脑此时会知道当前步最差也不会小于1,然后是0,那么0对应子树就可以忽略了(因为不可能好过1),接下来是3,所以电脑此时会知道当前步最差也不会小于3,然后看2,2对应子树也被忽略了(因为不可能好过3)。
好了,mapmin和omit已经解释得有点啰嗦了,就此打住。
走到这一步,evaluate函数可以改写为:
1 | evaluate = max.maximize’.maptree static.prune 8.gametree |
正是有了惰性求值,evaluate函数才能高效地执行,并处理无限层次的树。maximize’如前所述,也能够提高效率,因此使得我们有能力处理更深的树(原来我们设定的是5层,现在可以改大点,如8层)。
evaluate函数还可以继续优化。
看刚才这个大例子,mapmin [[1,2], [0,6], [3,5], [2,3]],如前所述,实际处理的是[1,0,3,2]。[1,0,3,2]会忽略掉两个子树。如果这个列表顺序改变一下呢?例如变为[3,2,1,0],显然会有三个子树被忽略。因此,我们可以将该列表先排序,将最大的排在前面。
1 | highfirst (Node n sub) = Node n (sort higher (map lowfirst sub)) |
这里,higher定义了如何比较两个子树,highfirst和lowfirst轮流调用(它们分别作用于相邻的层),最后的结果是这棵树某一层的子树都是大的排在前面,下一层都是小的排在前面,接下来的一层又是大的排在前面,如此往复直到叶子节点。
加上这个优化,evaluate函数可以改写为:
1 | evaluate = max.maximize’.highfirst.maptree static.prune 8.gametree |
这样highfirst处理完之后,maximize’处理的列表是排好序的,当然,我们可以只处理前几个(比如前3个)。这样,我们将highfirst处理后的树做些改变,将每个节点的子树只保留三个(不是只取一个的可能的原因是,若干子树具有相同的最优值),剩余的直接删掉。这样的话,效率有可能会有进一步的提高。
修改树的操作为:
1 | taketree n = foldtree (nodett n) Cons Ni |
其中take n list 会保留list的前n个元素,剩余的全部删除。
taketree的原理前文已经描述过了。
现在只需要将先前的evaluate表达式中higher替换为(taketree 3 higher) 就行了。
还有一个优化。现在的evaluate函数会prune固定深度,那么如果某个节点还想再往下看几步怎么办?我们将prune函数做些改变
1 | prune 0 (Node pos sub) = Node pos (map (prune 0) sub) if dynamic pos |
假设dynamic pos可以判定一个pos是否想继续往下看。
从我们分析和不断改进alpha-beta算法中evaluate表达式的过程,我们可以体会到,提供了高阶函数和惰性求值的FP语言是如何轻松地完成的,此时,我们应该确实能体会到高阶函数和惰性求值带来的模块化能力了。
结论
模块化对编程很重要,模块化(modularity)不仅仅是模块(module)。
我们将问题拆分的能力直接依赖于我们如何将子问题的结果结合(glue)起来。
FP提供了两种模块化能力—高阶函数和惰性求值,这提供了新的有用的模块化编码方式。将程序看做若干通用函数和特化函数的结合,通用函数带来了强大的复用和模块化,这也使得FP代码简短易写。
扫描二维码,分享此文章
