《EFFICIENCY IN THE COLUMBIA DATABASE QUERY OPTIMIZER》 1998
这是Portland State University的硕士论文,作者是YONGWEN XU,相比Cascades论文的跳跃和晦涩,这篇可以说是很良心了。
Motivation
当时背景下,优化器仍然是值得研究的方向,尤其是在Decision Support Systems(DSS)、OLAP、大数据量、复杂对象、新的执行技术如并行和分布式执行等等。
第一代可扩展的优化器包括EXODUS、Starburst等,模块化和可扩展比较好,但搜索性能不太好。第二代如Volcano,使用了physical property来引导计划的搜索。第三代如Cascades,使用了面向对象的设计来简化实现。
这三代优化器可以分为两类,一类是自下而上的动态规划(bottom-up dynamic programming)优化器,如Starburst,另一类是自上而下的分支定界的基于代价的规则驱动(top-down branch and bound rule-driven cost based)优化器,如Cascades。
Columbia优化器类似Cascades优化器,并在其基础上进行了改进。
Terminology
Query Processing大致过程
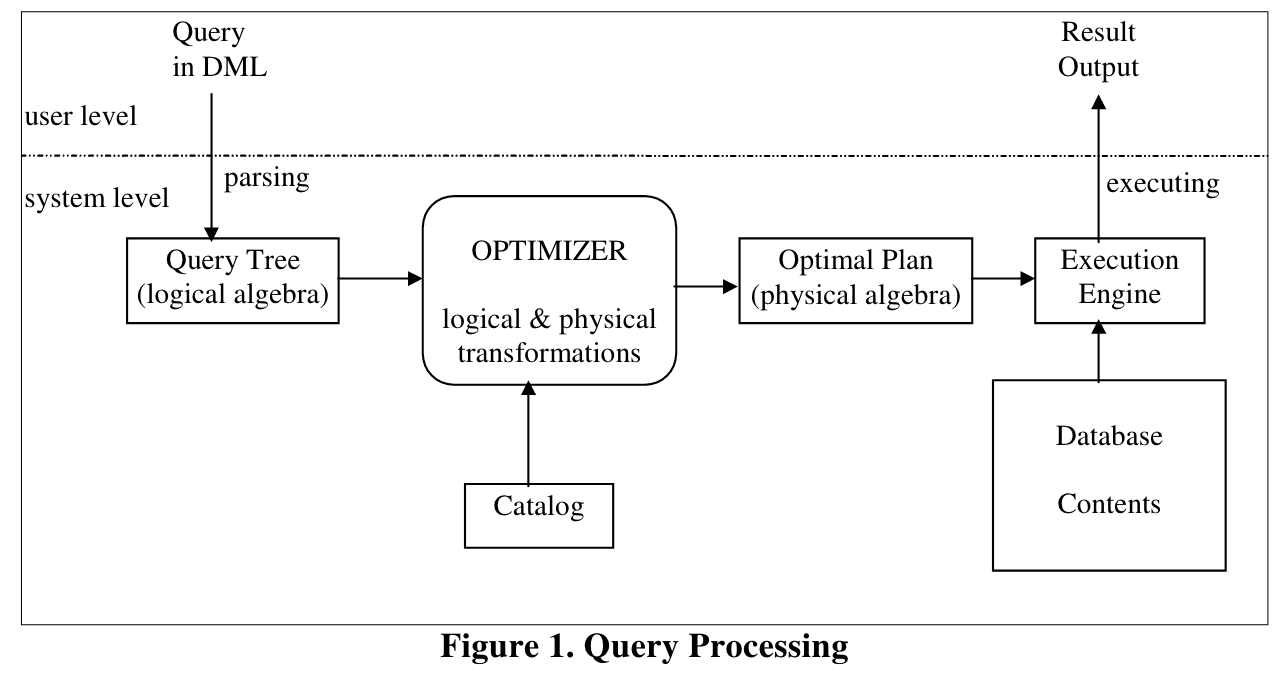
Groups
Query Tree :逻辑执行计划树
Excution Plan :物理执行计划
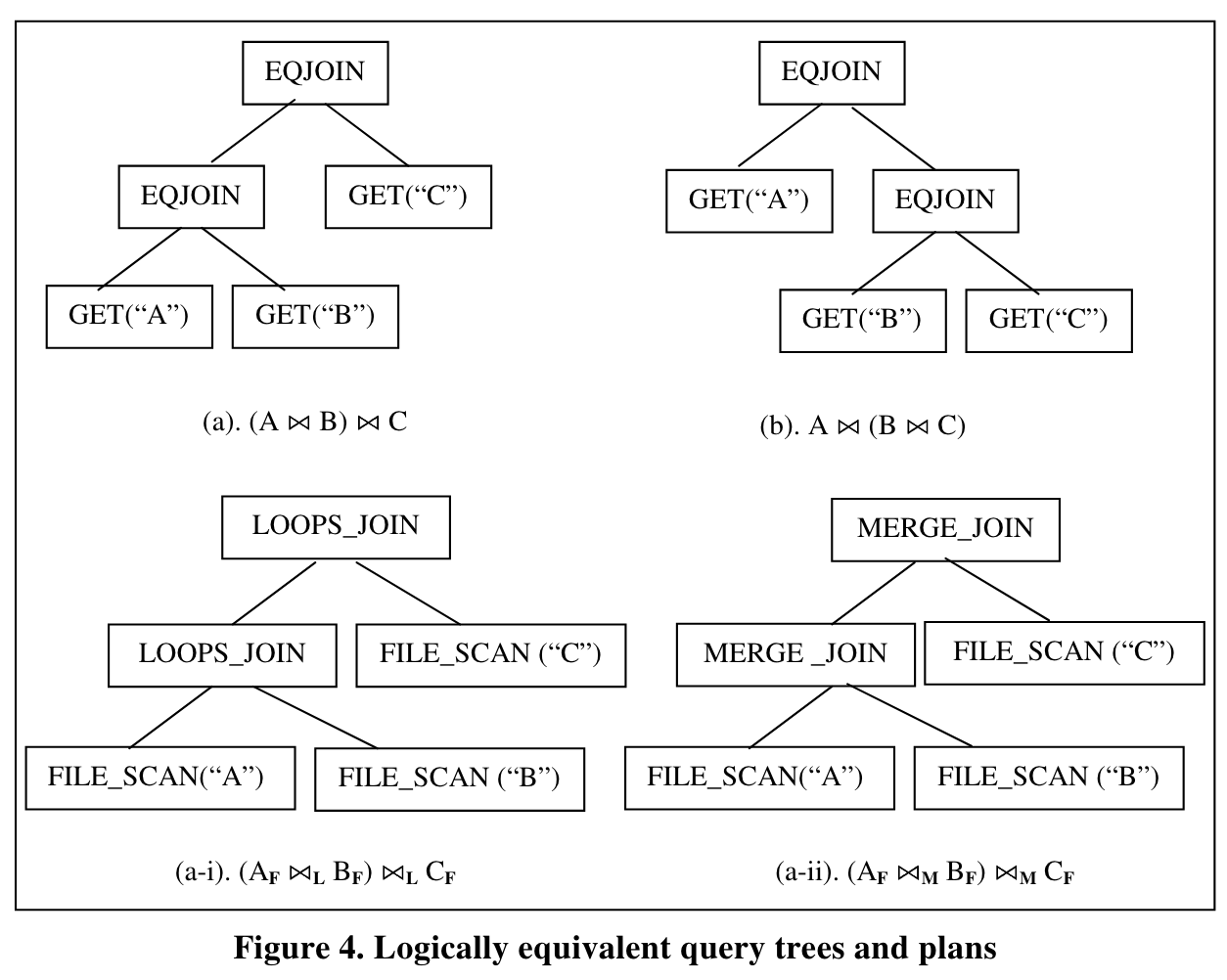
Expression :query tree(或者sub tree)和excution plan(或者sub plan),实际上就是逻辑和物理计划的混称,也分别称为logical expression和physical expression。
Group :logical expression的所有等价的expression称为一个Group,自然是包括logical和physical expression。
例如A⋈B⋈C,也写作 [ABC]的group如下:

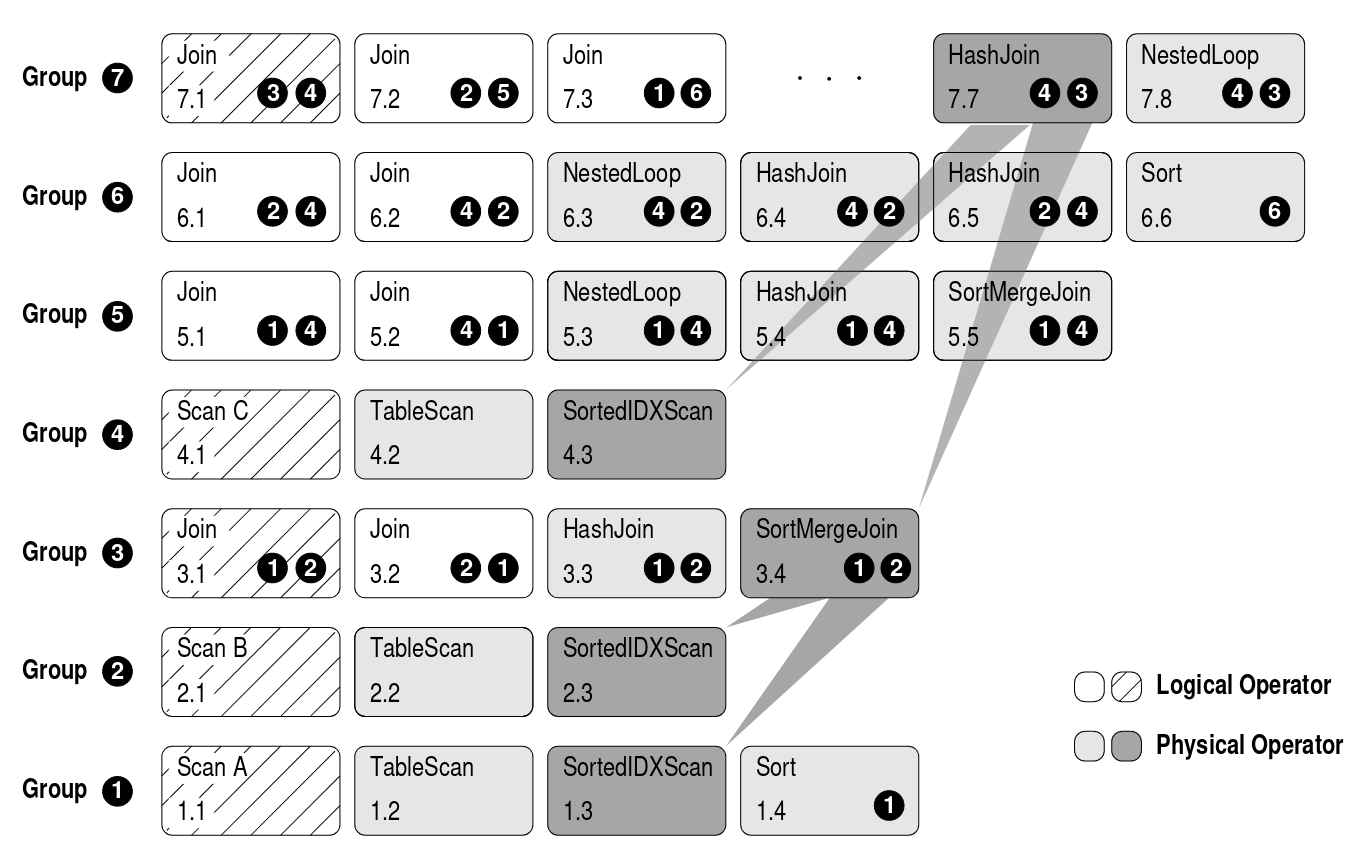
Multi-expression :,简写mexpr,这是基于group的一个抽象概念,是指以group为输入的逻辑算子或者物理算子。例如[AB]⋈C就是group [AB]和[C]的EQJOIN表达式。
例如group [ABC]的所有的multi-expression如下。

引入Multi-expression的好处是可以节省大量搜索空间,如上例中,[AB]就作为一个整体。
Search Space
给定一个查询,其所有等价的logical query tree和physical plan构成一个搜索空间。搜索空间用group来组织以节省空间,每个group以其他group作为输入。
其中final group也叫top group,它对应整个查询的执行结果,相应地,它的EQJOIN也叫top operator。operator映射到search space中的node,从初始的查询可以容易地映射到初始搜索空间(initial search space)。
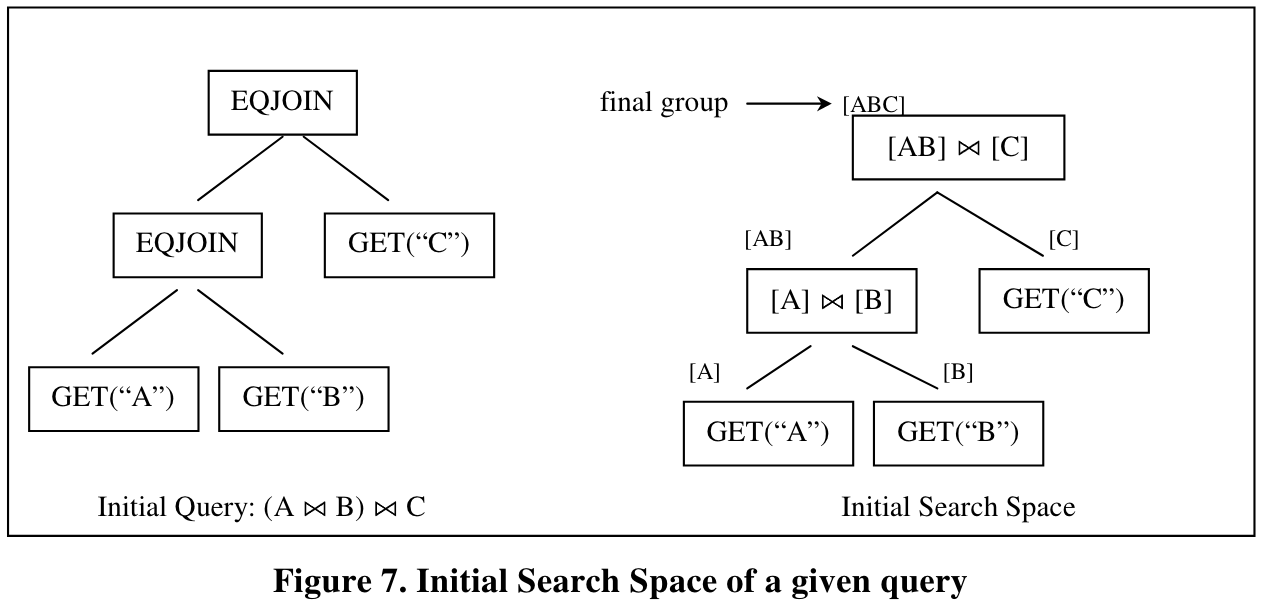
假如我们需要找到全局最优的physical expression,则需要生成所有的physical expression及其cost,因为一个physical expression是某个logical expression的一种实现方式,因此这意味着需要生成所有的logical expression。当全部的physical expression及其cost都生成之后对应的完全扩展开的search space叫做final search space,也就是锁final search space包含了输入查询的所有等价expression(logical and physical)。
search space大小:
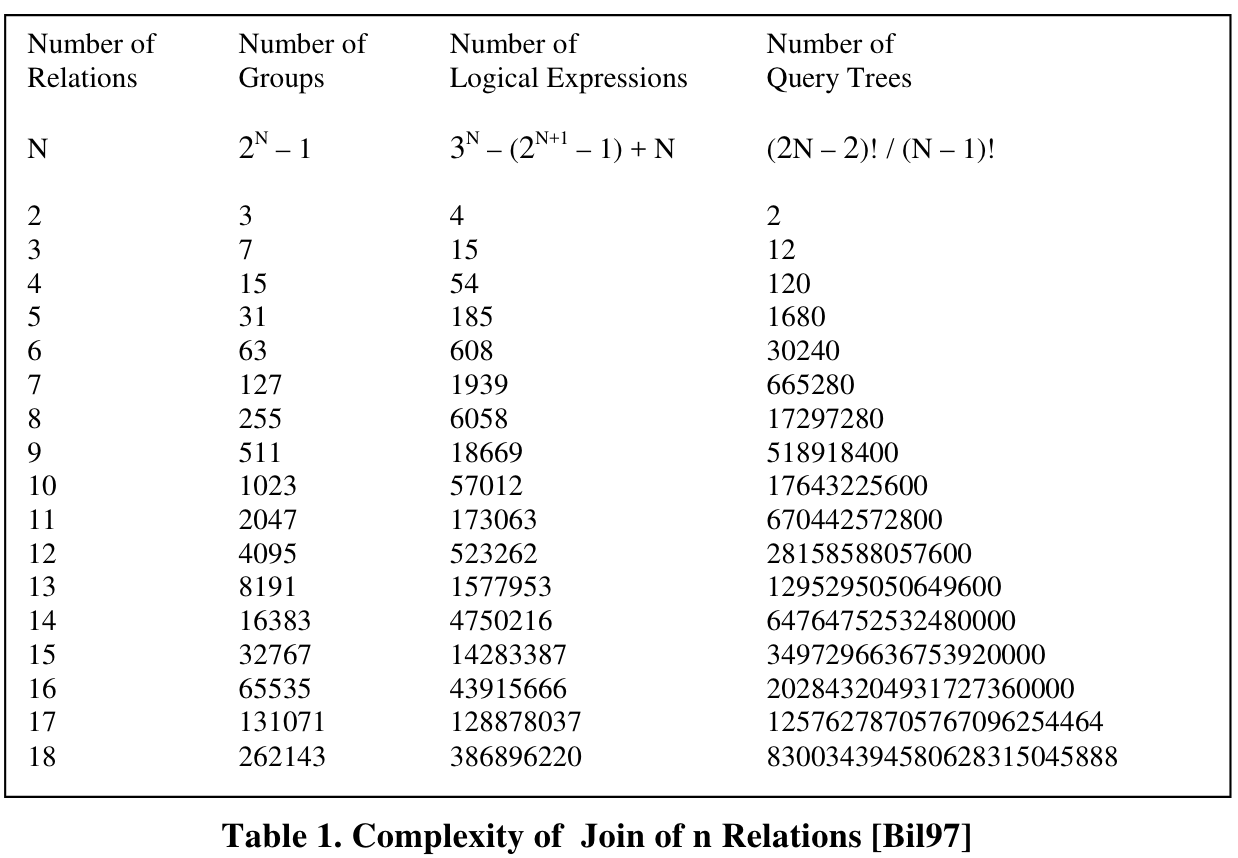
Rule
规则包括pattern和substitute。从logical expression到logical expression的规则称为transformation rule,从logical expression到physical expression的规则称为implementation rule。
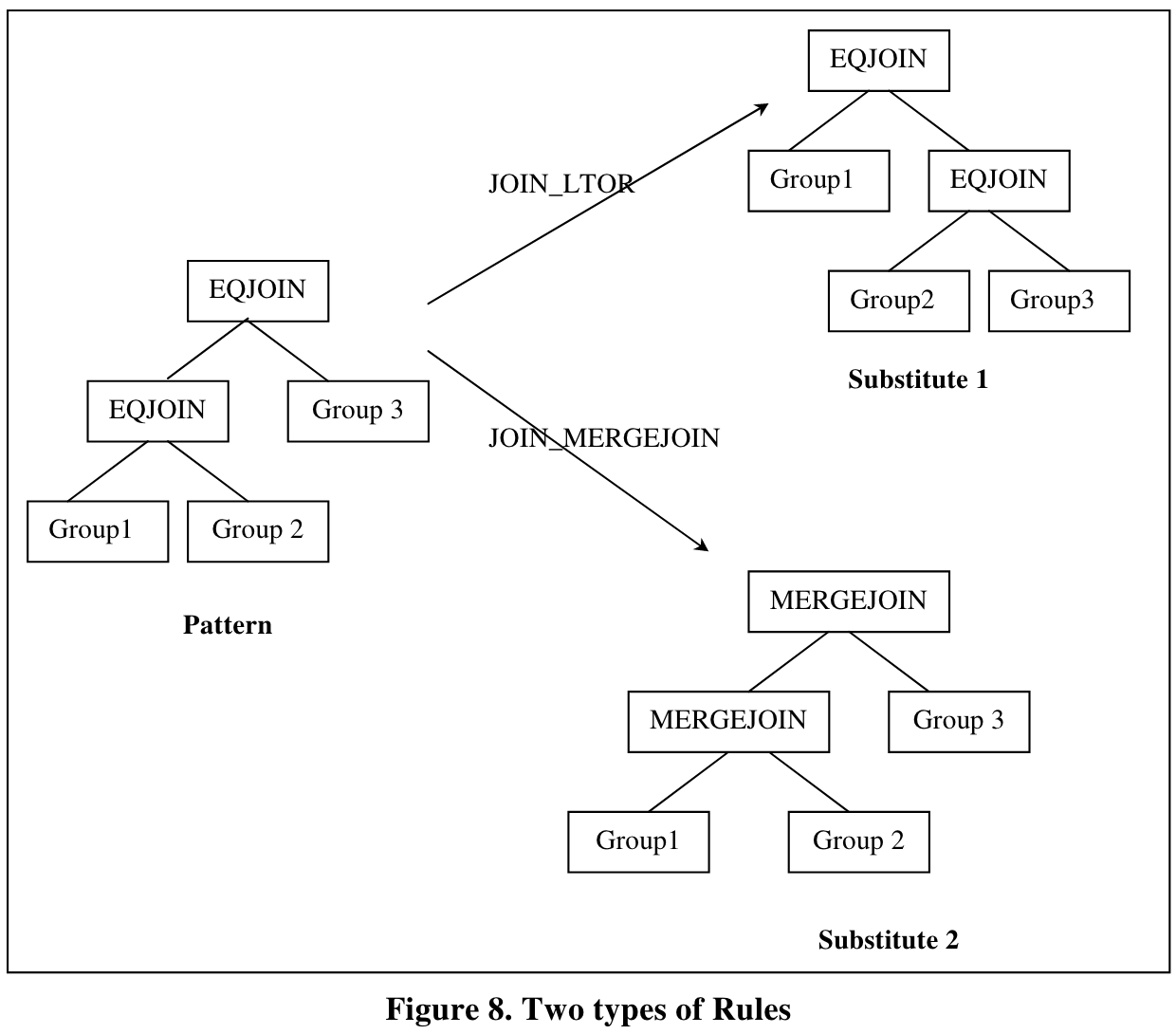
Related Work
System R and Starburst
对应的两篇论文《Access Path Selection in a Relational Database Management System》和《Starburst Mid-Flight: As the Dust Clears》。
Sysmtem R是cost-based优化器,采用了bottom-up动态规划搜索策略。所谓bottom-up是指当优化时先考虑低层次的expression。为了计算一个expression的最优代价,要先计算该expression的所有输入的低层次expression的cost。其计算量是指数的,因此System R也会采用一些启发算法或者搜索时某些情况下只考虑其中一些可能性。
Starburst包括两个基于规则的子系统,查询重写Query Graph Model (QGM)优化器 和 plan optimizer。
QGM是系统表达查询的一种数据结构,QGM优化器采用一组规则将一个QGM转成另一种更好的QGM,生成的QGM更通常更优或者更容易被进一步用基于代价的方式优化,见先前的博文介绍。
Plan optimizer是一个select-project-join优化器,包含join enumerator和plan generator。
Starburst优化过程即包括两个阶段,一是QGM optimizer的rewrite,二是plan optimizer生成access plan。
Starburst的QGM优化器可以处理复杂的启发优化,但这里只使用了逻辑信息而没有代价信息,另外也只能处理关系代数的操作而不能扩展至非关系代数操作。
Exodus and Volcano
Exodus是第一个使用top-down的可扩展优化器框架,其输入是模型描述文件(描述operator)、构建和比较access plan时的一些属性函数、transformation rules、implementation rules。Exodus的主要贡献是优化器生成器框架将搜索策略和数据模型拆分开、将transformation rules和implementation rules拆分开。
Volcano旨在提高Exodus的效率,将动态规划和基于physical properties的directed search、分支定界剪枝和启发式引导整合到搜索算法中,称之为directed dynamic programming。这也是一个top-down的goal-oriented(面向physical properties为goal)策略,sub expression按需优化,只有那些确定在比较优的计划中的sub expression才会被优化。Volcano已经被用于面向对象数据库产品和科学计算数据库系统中,证明了其可扩展性。
Cascades
Cascades是在Exodus和Volcano的基础上的改进。
一些优化点:
- 将优化任务组织为数据结构
- 将规则作为对象
- 放置property enforcer的规则
- 搜索执行下一步时根据promise排序move
- 谓词作为operator(既可以作为logical也可以作为physical)
- 允许DBI(database implementor,也就是Cascades的用户)自定义接口和子类型层次的一套抽象接口类
- C++语言编写,接口实现上抽象的好
- tracing support和更好的文档来帮助DBI
优化过程被拆成task,实现上task对应一个对象,包含一个perform函数。Task存放在LIFO Stack中,执行时从栈顶取一个task对象执行,执行过程中可能产生新的task对象压入栈。Cascades优化器从初始query开始,触发优化top group,进而触发逐个更小的sub group的优化,group的优化即找到group中最好的plan。这个过程中除了新的task生成并压入栈之外,新的group和expression也会产生,当top group完成后,优化就结束了。
和Volcano是一样,Cascades也是top-down搜索策略,也使用动态规划和memorization,一个expression在优化时,先看memorization中之前该expression有没有做过优化。但和Volcano不一样的是,Cascades是按需对group进行探索,Volcano是先穷尽所有的logical expression然后再开始physical expression,Cascades并不将这两步拆开。Cascades用户接口比Volcano也更友好。
Cascades也存在一些问题,如optimizer framework和DBI的specification割裂、虚函数太多、对象分配释放太频繁,这些都会带来性能问题。另外有些剪枝技术可以应用到top-down优化器上。这也是Columbia优化器的优化目标。
Structure of the Columbia Optimizer
Overview of Columbia Optimizer
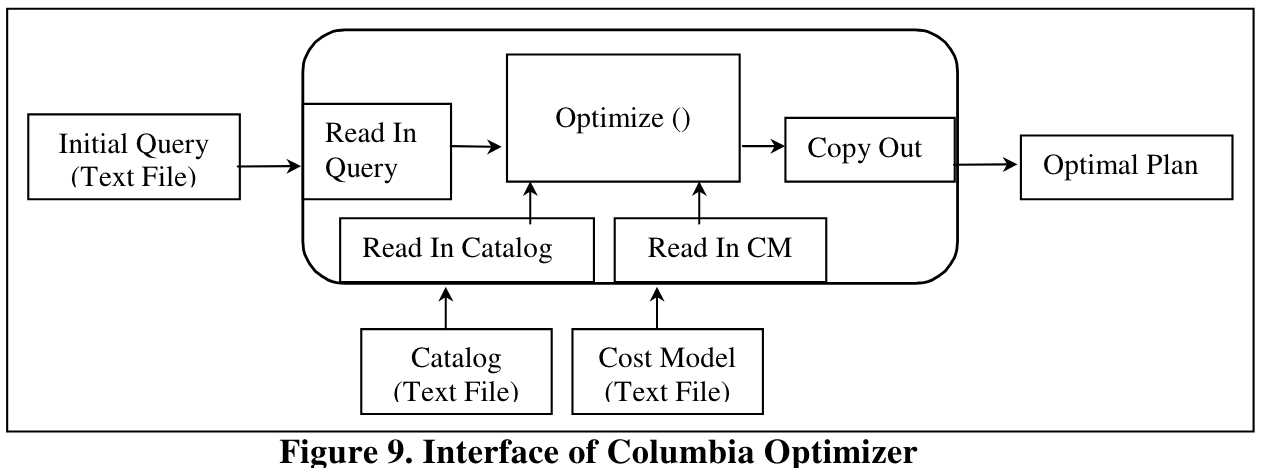
输入是以文本的形式表达的expression,类似于LISP风格,其目的是解耦parser和optimizer,提高可扩展性。
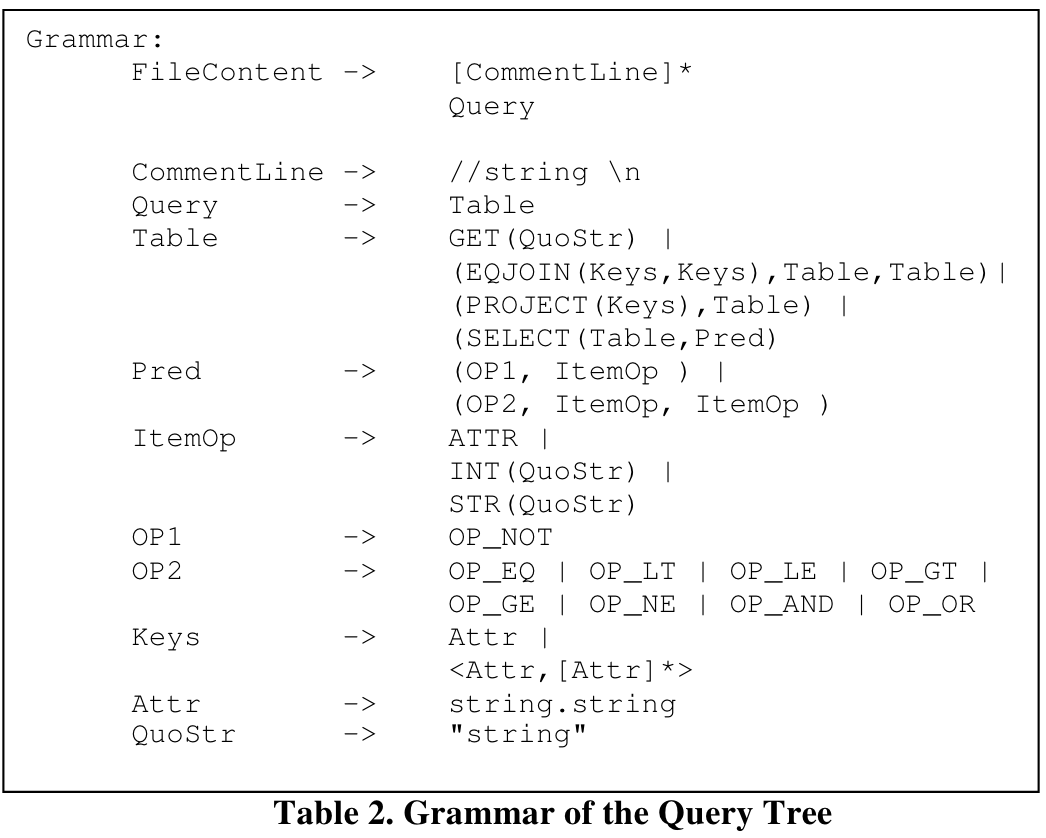
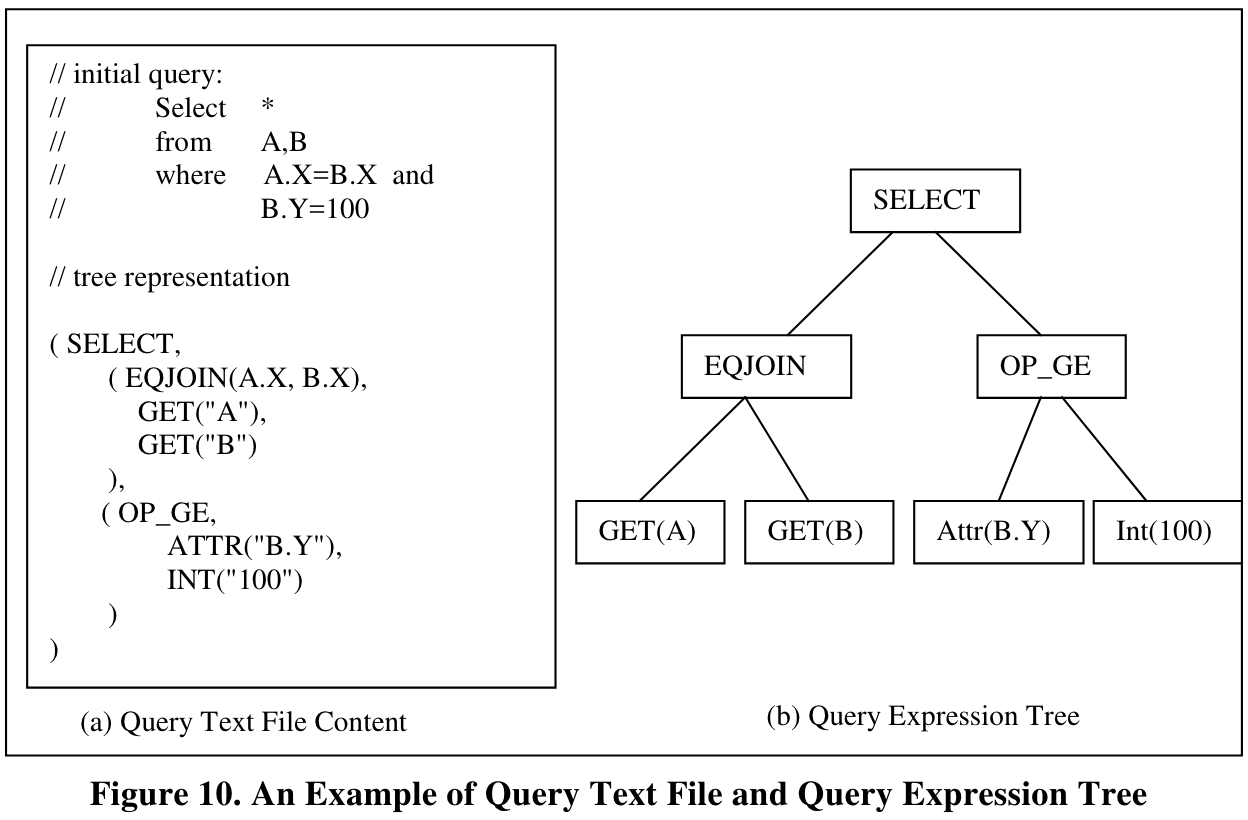
输出是以缩进的physical expression的tree形式表达。

另外两个外部依赖是Catalog和Cost Model,它们也都是以文本形式存放的,优化器读入文本,并将内容分别存入全局对象Cat和Cm(CAT类型和CM类型的对象实例)。
Search Space
Search Space Structure - SSP
Columbia使用SSP类来表示search space,SSP类似于Cascades的MEMO。SSP包含一组Group,每个group包含一组逻辑上等价的multi-expression。
初始的时候,只有initial group,优化过程会增加新的group和multi-expression逐渐扩展search space,所以其除initial group外其他group都是另外某个group的input group。
CopyIn函数用于将expression拷贝到search space中的multi-expression,CopyOut用于将最终结果拷贝出来。
Multi-expression去重
去重用的搜索结构,可以是一个搜索树、动态或静态hashtable。Columbia用的是静态哈希表,multi-expression的所有组件,包括算子、操作参数、input group,都会被hash到hashtable用来查重。
Columbia实现上,FindDup函数负责查找并返回重复的multi-expression。
class GROUP
实现上,class GROUP用于表示group类型,因为所有的multi-expression的logical property都是一样的,所以GROUP持有一个指向logical property共享对象的指针。
与Cascades相比,Columbia做了几个优化:
- group代价下界
- 区分logical和physical multi-expression
- 存放winner group的数据结构优化
group代价下界
用于剪枝,如果一个group的代价下界越高,可能被剪枝。
那么下界如何估算呢?
首先是一些基础定义:
- **touchcopy()**函数:表示join操作读取两个输入表的各一行并输出一行结果的代价
- **Fetch()**函数:从磁盘读取一个字节的平摊开销
- **|G|**:group G的cardinality
- **cucard()**函数:设表A是Group G涉及到的表,A.X是涉及到的列,则cucard(A.X)表示A.X列上unique cardinality,cucard(A)表示所有涉及到的列的cucard最大值。
计算lower bound的公式:

其中,”from other non-top joins” 的部分可以简单理解为{Ai}按升序排列,左深树join方式的最低代价值。对此项和fetch项,论文也给出了较为完善的证明过程,读者可以自行阅读。
区分logical和physical multi-expression
Cascades是将二者保存在同一个list,Columbia是分开在两个list中。
分开在有些情况下更好:
- rule bindings只需要检查logical multi-expression,分开可以减少访问的内存次数
- 如果我们在已经优化过的group上,为另一个不同的property(例如要求在另一列上有序)进行优化,则对二者处理不同:扫描physical multi-expression检查desired property是否满足条件及计算代价;扫描logical multi-expression检查是否有合适的规则可以应用,只有存在某个规则之前没被应用过,才需要对logical multi-expression应用规则优化。在这种为另一个property进行优化的场景下,Cascades会对logical multi-expression重新进行优化。
存放winner group的数据结构优化
winner是指在特定优化条件(例如要求结果在某列有序,代价小于某值)下,一个问题或者子问题的最优结果。同一个group在不同条件下会有不同的winner,所以group结构里面有一个winner的列表。
Cascades的数据存储方式是,每个winner及其对应的优化条件作为一对存放,每对用链表连接。
Columbia的数据存储方式是,用winner结构体数组来表示,每个winner结构体包含一个multi-expression、代价和对应的physical property。winner结构体比较通用,也能用于保存搜索的中间结果。
1 | class WINNER |
Expression
Expression有两个类型,EXPR和M_EXPR。
EXPR表示查询或者子查询,包含一个operator(class OP)及其参数、input expression(class EXPR)。
M_EXPR表示multi-expression,M_EXPR包含一个operator、input group(EXPR是input expression)。
M_EXPR是group的主要组件,搜索也是面向M_EXPR来的,因此M_EXPR会有一些搜索相关的状态信息。
1 | class M_EXPR |
Rules & BINDERY
Rule实现上用**class RULE**来表示,成员包括 rule name、antecedent(规则应用前,即pattern)、consequent(规则应用后,即substitute)。Pattern和substitute都用expression(class EXPR)对象来表达。
举个例子:
1 | Pattern ( L(1) JOIN L(2) ) JOIN L(3) |
这里,L(i)表示leaf operator,它在pattern和subsitute中没有其他输入,实际上可能是其他sub tree。
应用某条rule时,首先是将rule的pattern绑定到Search Space中的mexpr,这是由BINDERY类来完成的。
比如这样一个 mepxr [G7 JOIN G4] JOIN G10 ,其中,Gi是Group ID为i的Group, [G7 JOIN G4]是search space中的gruop,它的一个binding是 L((1)绑定G7,L(2)绑定G4,L(3)绑定G10。
BINDERY负责生成所有类似这样的binding。BINDERY会对每一个input subgroup生成一个BINDERY对象,例如LTOR rule,会生成一个左input的bindery和右input的bindery。其中左input会找到两个binding,G4 JOIN G7 和 G7 JOIN G4(都是[G7 JOIN G4]的mexpr之一)。
**APPLY_RULE::perform()**函数驱动上述BINDERY生成binding,并生成新的mexpr。后文会提到,O_EXPR中会尝试apply各个rule(各自创建一个APPLY_RULE对象)。
RULE还有两个重要函数:
- top_match() 函数是用于判断当前rule与expression的top operator是否相同,用于快速判断rule是否可以匹配expression的pattern。
- promise() 函数根据优化上下文返回一个promise value,该值越大表示越应该尽早应用该rule,小于等于0表示不要应用;默认implementation rule更大一些。
Enforcer
enforcer是为了获取某些物理属性而新插入的物理算子,例如qsort operator。enforcer以group为输入,输出是相同的group但其物理属性变化了。
例如一个SORT_RULE:
1 | Pattern: L(1) |
例如 MERGE_JOIN(A.X, B.X), G1, G2 ,要求G1在A.X上有序、G2在B.X上有序,也就是search context要求G1和G2需要具备有序属性时,应用该SORT_RULE。
Columbia和Cascade在这里的实现上有两处差异。
一是 excluded property:Cascade用的是excluded property来避免重复apply enforcer,Columbia用的是RuleMask。
二是 enforcer的表示方式:Cascade里面enforcer是一个有参数的物理算子,Columbia中是不带参数的物理算子。
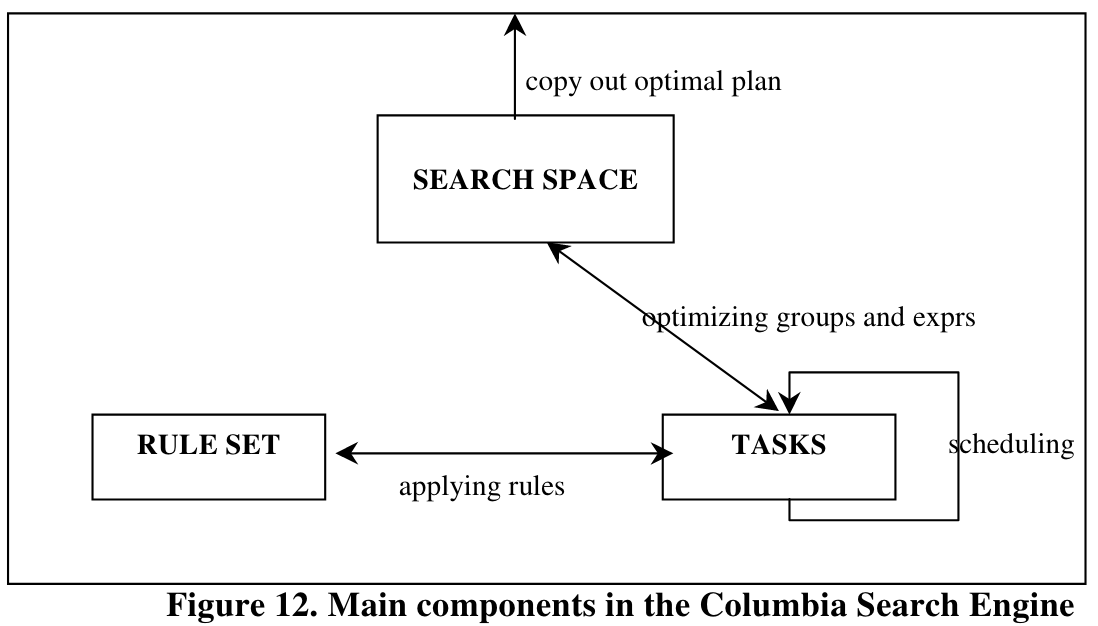
Task
Task是搜索过程的执行单元,第一个task是优化整个查询,task可能会生成并调度新的Task,直到task都执行完,优化结束。
实现上,class TASK用来表示task的抽象类,有一个context成员和一个perform()函数。class PTASK表示pending task,即待执行的task类型,所有的PTASK对象用栈(变量名PTasks)组织起来,第一个PTASK对象即是优化top group,也就是优化整个查询的task。
1 | optimize() |
Task有几种子类型:
- O_GROUP :group optimization
- E_GROUP :group exploration
- O_EXPR :expression optimization
- O_INPUTS :input optimization
- APPLY_RULE :rule application to a mexpr
其关系如图,其中A->B箭头表示A调用B
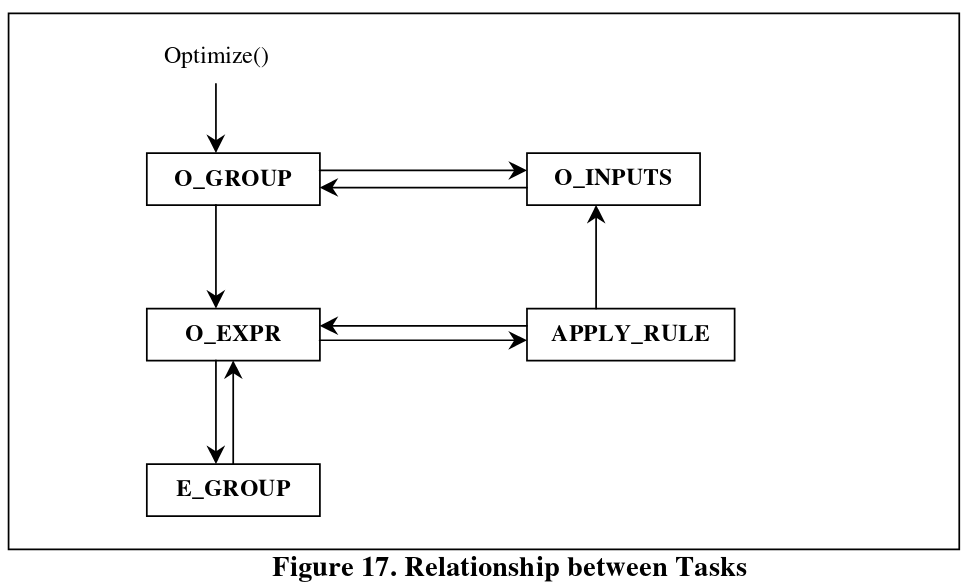
O_GROUP
该类型的task是在给定context下,找到group内的最优计划,并将结果存入group的winner成员中。该任务会生成该group的所有的logical expression和physical expression,计算所有physical expression的代价。O_GROUP task会创建O_EXPR和O_INPUT。
O_GROUP的主要逻辑:
1 | O_GROUP::perform(context) |
E_GROUP
考虑join的左结合rule,当mexpr的join operator匹配到join后,需要展开group的左输入group看是否满足左输入有join的条件,所有的左输入join需要都满足rule的join才能应用这个rule。
E_GROUP通过创建所有的目标logical operator来展开group。
1 | // 对于匹配的pattern,生成所有的logical mexpr |
O_EXPR
O_EXPR有两种目的,task上有flag(optimizing / exploring)来区分二者。
一个目的是优化mexpr,O_EXPR会将rule set中的所有rule都尝试触发,触发按照promise顺序来。transformation fule用于扩展express,生成新的logical expression,implementation rule用于生成相应的physical expression。
另一个是探索mexpr来准备rule matching,这种情况下task仅针对logical expression进行扩展,也就是只使用transformation rule。
1 | // optimize或explore一个mexpr,触发所有合适的rule |
APPLY_RULE
该task用于将rule apply到logical mexpr,生成新的logical或者physical mexpr。
1 | // apply transformation rule或者implementation rule |
O_INPUTS
该task用于计算physical mexpr的代价。计算过程大致是先计算所有输入的mexpr的代价,然后累加到top operator的代价上。
该task的执行过程伪代码如下:
1 | G: 待优化的group; |
1 | /* |
Pruning Techniques
剪枝主要用在O_INPUTS task中。
Columbia优化器介绍了两种剪枝技术:Lower Bound Group Pruning、Global Epsilon Pruning。这里用例子说明一下。
Lower Bound Group Pruning
比如现在优化器的输入是 (A⋈B)⋈C,优化器算出了其中一个plan的代价,比如 (A⋈LB)⋈LC代价是5秒,则继续搜索最优计划时,如果expand到group [AC]⋈L[B],假设[AC]是要计算笛卡尔积,其代价超过5秒,那么[AC]的所有计划都不会再被生成了。
Global Epsilon Pruning
它的含义是,有时候我们不是一定要找到最优的plan,而是找到一个满意的plan就可以。
扫描二维码,分享此文章
