《挑战程序设计竞赛》读书笔记(一)搜索 回溯
本文阅读了《挑战程序设计竞赛》前几页,写了部分读书笔记。对其中一些例题增加了新的解法,文中增加了图示效果帮助自己和读者加深理解,扩充了回溯等算法,增加了回溯中搜索子集树和排列树的框架。
超哥之前推荐过《挑战程序设计竞赛》一书。书名虽然说是应对竞赛,但该书同样适合于像我这样的普通的程序员用来提高一下算法能力。
今天读了几页,感觉收获很大,希望将来能够啃完,同时推荐给各位读者。
关于运行时间的估算
对于复杂度为O(n2)的算法,如果n<=1000,则要执行106次。如果时间限制是1s,则通常有如下表的判断。
| 10^6 | 游刃有余 |
| 10^7 | 勉勉强强 |
| 10^8 | 很悬,仅限循环体很简单的情况 |
1.6热身题
1.6.1章节给了一道热身题。
题目描述如下:有n根棍子,长度已知为ai(i=1,2,…n)。想要从中选出三根棍子,组成一个周长尽可能长的三角形。要求输出最大周长的值,如果不能组成三角形则输出0。
比较容易想到的是O(n3)的算法。书中提到有O(nlogn)的算法。我的解法如下,望读者批评指正。
先降序排序,依次考察连续三个数。若能形成三角形,则这个三角形周长最大;否则继续考察下一个连续三个数。
证明:设排序之后的结果为a1 a2 a3 a4 a5 … an。如果a1 a2 a3能组成三角形,无疑该三角形周长最长。如果a1 a2 a3不能组成三角形,则说明a1 >a2 +a3 ,那么 a1 是不可能出现在任何三角形中的,因为a2 +a3 已经是剩余数中和最大的两个数了。所以a1 被排除。迭代该方法,不断地排除当前剩余的数中最大的数,直到剩余的数中最大的三个数能够形成三角形,则这个三角形就是所求的三角形。
该算法复杂度:
排序O(nlogn) + 迭代O(n) = O(nlogn)
1.6.3章节给了一个抽签的例子。
题目大意:长度为n的数组,从中有放回地取出四个数字,问是否存在4个数字,其和为M。
书中给出了O(n4),O(n3logn),O(n2logn)三种算法。
O(n4):最naïve的方法。四重循环。
O(n3logn):三重循环 + 二分查找。
O(n2logn):对于想找出是否存在a,b,c,d使得a+b+c+d=M,我们预先计算出c+d的所有n2个和,并排序后放在新的数组S中。循环a,b,在数组S中二分查找。该算法空间复杂度为O(n2)。
应该还有一个O(n3)的算法。
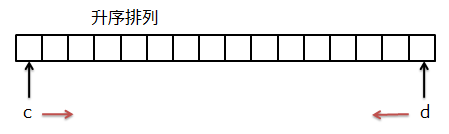
在指定了M-a-b的值之后,查找满足c+d=M-a-b的c和d时,可以预先将原数组排序,然后令c和d分别从数组首尾两端开始向中间移动。如图示。
记M-c-d为K。如果c+d <K,说明当前的c不会被选择,因为连最大的d都不能配合它,所以c向前走。同样,如果c+d>K,说明当前的d不会被选择,d也向前走(c和d的前相反)。因此O(n)时间内可以确定是否有合适的c和d。外层循环a,b,内层相向查找c+d,复杂度是O(n3),比O(n2logn)算法差,但空间复杂度为O(1)。
2.1穷竭搜索
常见的搜索方法有深度优先搜索(DFS)和宽度优先搜索(BFS),对应辅助的数据结构为栈(Stack)和队列(Queue)。
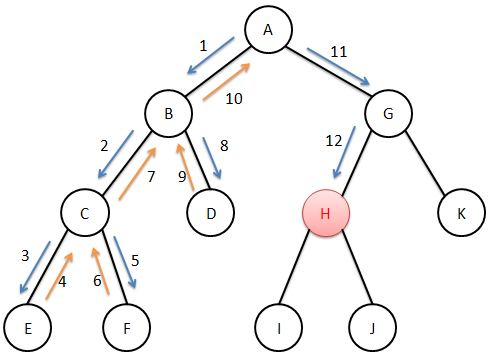
深度优先搜索(DFS):从当前状态开始,向下转移到下一个状态,直到状态无法向下转移,这时回退到前一状态,继续转移到另一个下一状态,直到找到最终的解。如图示。
初始状态为状态A,状态H为最终的解。
A -> B -> C -> E 此时状态E不能继续向下转移,则回退到C继续向C的下一个状态F转移。
在上图这个例子中,DFS搜索过程如图中数字和箭头所示。
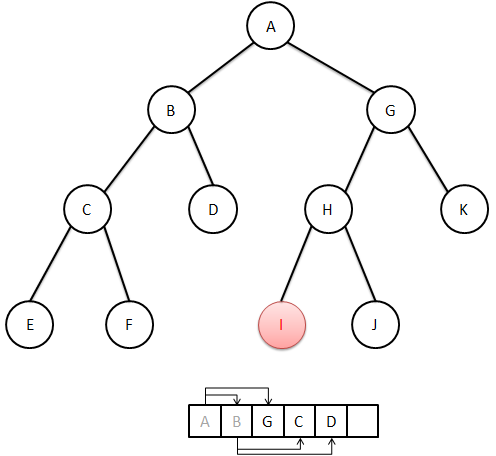
宽度优先搜索BFS:总是先搜索最近距离的状态。BFS借助队列Queue,执行过程大致如下,首先将初始状态加入Queue,然后不断地从Queue中取出队列首部的状态,将该状态的最近邻居加入队列,如此往复,直到取空了队列或者找到了解。如图示(图中此时队列已经删除A和B)。
状态如果简单,可以是一个整形或者pair等;如果状态复杂时,通常要封装成一个类来表示一个状态。
在多本算法教材上,都介绍了回溯。回溯(backtrack)是最常见的搜索算法。本文综合另外两本算法教材(见文末参考),在这里补充回溯的相关知识。
回溯法是“通用的解题法”,可以用来系统地搜索一个问题的所有解。与其说回溯是一个算法,不如说它是一个算法框架。
回溯法有三个非常明确的步骤:
1. 定义解空间,它包含了所要求的解。
2. 用合适的搜索方法来组织解空间。
3. 搜索(通常是DFS)解空间。
最常见的搜索有搜索子集树和搜索排列树。
搜索子集树。子集树是一个给定的集合的所有子集形成的解空间。例如,子集和问题(sum-of-subset)。子集和问题是说,给定一个数字集合,要求找到一个子集,使得该子集的数字之和为给定的C。
搜索子集树算法的框架如下。
|
1 2 3 4 5 6 7 8 9 10 |
void backtrack(int t){ if(t>n) Output(x); else for(i=0;i<1;i++){ x[t]=i; if(Constraint(t) && Bound(t)) backtrack(t+1); } } |
其中, x是01数组,x[t]=0(或1)分别表示第t个元素不在(或在)所求子集中。
Output(x)输出这个01数组,也就是对应一个子集。
Constraint(t)用来检查这个t是否能加入(不加入)子集,这个跟具体的问题有关。
Bound(t)用来检查是否出现了越界,便于剪枝,例如子集和问题中如果所有的数字都是正数,如果当前集合加入t之后已经超出给定值,则Bound函数返回False,不必再继续搜索了。
这个框架的原理就是分别设置x[t]=0和x[t]=1,然后分别向下递归。
搜索排列树。排列树是指所有的排列形成的解空间。旅行商问题是典型的排列搜索问题。旅行商问题描是指在一个加权的网络中,找到包括所有定点的最小权重的环路。通俗地说法就是想去N个地点旅行一遍,先后顺序怎么确定使得走的路途最短。
搜索排列树的框架如下。
|
1 2 3 4 5 6 7 8 9 10 11 |
void backtrack(int t){ if(t>n) Output(a); else for(int i=t; i<=n; i++){ swap(a[t], a[i]); if(Constraint(a) && Bound(a)) backtrack(t+1); swap(a[t], a[i]); } } |
其中,a表示顺序数组,里面存放的就是元素。在旅行商问题中,a就表示一个旅行顺序,例如,a=[C1,C4,C2...]。
Output(a)、Constraint(t)和Bound(t)与上类似。
该算法框架的原理如同打印所有排列相同。
本文用DFS搜索算法求解了一道小游戏--交换青蛙,详情请移步深度优先搜索求解青蛙交换位置小游戏。
参考:
计算机算法设计与分析(第三版),王晓东
数据结构算法与应用--C++描述,Sartaj Sahni著,汪诗林,孙晓东等译